Triangle split
Weekly Problem 50 - 2008
The lengths SP, SQ and SR are equal and the angle SRQ is x degrees. What is the size of angle PQR?
The lengths SP, SQ and SR are equal and the angle SRQ is x degrees. What is the size of angle PQR?
Age
11 to 14
Challenge level
Problem
In the diagram the length $SP$, $SQ$ and $SR$ are equal and the angle $SRQ$ is $x^\circ$. What is the size (in degrees) of the angle $PQR$?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Since $SP = SQ$, the triangle $PSQ$ is isosceles. Therefore, $\angle SPQ = \angle PQS$. We denote the measure of those angles by $y$. Similarly, $\angle SQR = \angle QRS = x^\circ$.
Image
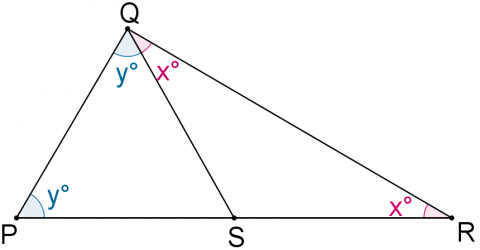
Since the sums of the interior angles of $PQR$ is $180^\circ$, $x + y + (x+y) = 180$, so $ 2x+2y=180 $.
Therefore, $ \angle PQR = x^\circ+y^\circ=90^\circ $.