Transformation ... or Not?
This graph looks like a transformation of a familiar function...
Problem
Do we always get new functions from old ones?
Take a look at the graph below.
Image
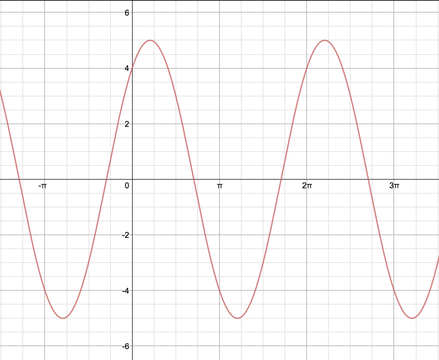
How would we describe it?
Can we describe it using a function we know?
This is an Underground Mathematics resource.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Underground Mathematics is hosted by Cambridge Mathematics. The project was originally funded by a grant from the UK Department for Education to provide free web-based resources that support the teaching and learning of post-16 mathematics.
Visit the site at undergroundmathematics.org to find more resources, which also offer suggestions, solutions and teacher notes to help with their use in the classroom.
Student Solutions
Vatsal from Wilson's School saw this function as a sin graph, and approximated its translation:
Similar to a sin graph, with a stretch by scale factor $5$ parallel to the $y$-axis
Translation of approximately $\frac{\pi}{4}$ units in the negative $x$ direction.
Hence, $y \simeq 5sin(x+ \frac{\pi}{4})$.
Louis from EMS and Timothy from Wallington Country Grammar both calculated the horizontal translation of the graph. Timothy writes:
The immediate graph that springs to mind is a sine graph, except this new
graph has two transformations: a stretch scale factor $5$ in the y direction
because the peaks are reaching $5$ and $-5$ and then the second is a shift
along the $x$-axis. This means the equation of our new graph will be of the
form:
$y = ksin(x+c)$
where $k$ is the s.f. of the stretch and $c$ is the shift along the $x$-axis.
k is 5:
$y = 5sin(x+c)$
Now we need to find $c$. From observation it is clear that the graph passes
through the point (0,4) so we can sub these values in and solve $c$.
$4 = 5sin(0+c)$
$sin(c) = \frac{4}{5}$
$c = arcsin(\frac{4}{5})$.
So adding this value to are equation we can reach the final answer of:
$y = 5sin(x+arcsin(\frac{4}{5}))$
Jack from Portsmouth Grammar School saw this function as a cosine graph, and approximated its translation:
You can solve these types of problems by firstly inspecting the maximum and
minimum values of the graph.
Since the maximum and minimum values of a
$y=cos(x)$ graph are $1$ and $-1$, the function must involve $y=5cos(x)$. The
function is the graph of $y=5cos(x)$ shifted to the right by approximately $\frac{\pi}{4}$. Therefore
you subtract $\frac{\pi}{4}$ from the $x$-coordinate, to give $y \simeq 5cos(x-\frac{pi}{4})$.
Jamie from Bentleigh Secondary College calculated the horizontal translation of $y=5cos(x)$:
$f(x-cos^{-1}(\frac{4}{5}))=5cos(x)$
This result was achieved by initially letting $f(x-z) = 5cos(x)$, and
beginning to look towards a mathematical approach to finding the offset.
The approach I used (for ease and effectiveness) was to solve for $z$ when
$5cos(x-z) = 4$ while $x = 0$. This led me to find that $z = cos^{-1}(\frac{4}{5})$.
Jamie also discussed the idea of 'new' functions:
The question 'Do we always get new functions from old ones?', is difficult
to answer. Sometimes we perceive that we have a new function from an old
one, an example being the quadratic formula's relationship with
$f(x)=ax^2+bx+c$, where we acknowledge the former being a separate one from
the latter, where it is just some 'rearrangement' of the same function.
Then in our example where the function was some transformation of the
cosine function, we are tempted to say that it is not a new function, just
some 'changing' of the original one, where widely accepted information
shows that it is.
My understanding is that every function that is 'transformed' from an old
one, is not a new one, but simply a different version of it, what that new
function does could be similar or different from its original, but
nonetheless, the same.
Thank you to everybody who submitted a solution to this problem!
Similar to a sin graph, with a stretch by scale factor $5$ parallel to the $y$-axis
Translation of approximately $\frac{\pi}{4}$ units in the negative $x$ direction.
Hence, $y \simeq 5sin(x+ \frac{\pi}{4})$.
Louis from EMS and Timothy from Wallington Country Grammar both calculated the horizontal translation of the graph. Timothy writes:
The immediate graph that springs to mind is a sine graph, except this new
graph has two transformations: a stretch scale factor $5$ in the y direction
because the peaks are reaching $5$ and $-5$ and then the second is a shift
along the $x$-axis. This means the equation of our new graph will be of the
form:
$y = ksin(x+c)$
where $k$ is the s.f. of the stretch and $c$ is the shift along the $x$-axis.
k is 5:
$y = 5sin(x+c)$
Now we need to find $c$. From observation it is clear that the graph passes
through the point (0,4) so we can sub these values in and solve $c$.
$4 = 5sin(0+c)$
$sin(c) = \frac{4}{5}$
$c = arcsin(\frac{4}{5})$.
So adding this value to are equation we can reach the final answer of:
$y = 5sin(x+arcsin(\frac{4}{5}))$
Jack from Portsmouth Grammar School saw this function as a cosine graph, and approximated its translation:
You can solve these types of problems by firstly inspecting the maximum and
minimum values of the graph.
Since the maximum and minimum values of a
$y=cos(x)$ graph are $1$ and $-1$, the function must involve $y=5cos(x)$. The
function is the graph of $y=5cos(x)$ shifted to the right by approximately $\frac{\pi}{4}$. Therefore
you subtract $\frac{\pi}{4}$ from the $x$-coordinate, to give $y \simeq 5cos(x-\frac{pi}{4})$.
Jamie from Bentleigh Secondary College calculated the horizontal translation of $y=5cos(x)$:
$f(x-cos^{-1}(\frac{4}{5}))=5cos(x)$
This result was achieved by initially letting $f(x-z) = 5cos(x)$, and
beginning to look towards a mathematical approach to finding the offset.
The approach I used (for ease and effectiveness) was to solve for $z$ when
$5cos(x-z) = 4$ while $x = 0$. This led me to find that $z = cos^{-1}(\frac{4}{5})$.
Jamie also discussed the idea of 'new' functions:
The question 'Do we always get new functions from old ones?', is difficult
to answer. Sometimes we perceive that we have a new function from an old
one, an example being the quadratic formula's relationship with
$f(x)=ax^2+bx+c$, where we acknowledge the former being a separate one from
the latter, where it is just some 'rearrangement' of the same function.
Then in our example where the function was some transformation of the
cosine function, we are tempted to say that it is not a new function, just
some 'changing' of the original one, where widely accepted information
shows that it is.
My understanding is that every function that is 'transformed' from an old
one, is not a new one, but simply a different version of it, what that new
function does could be similar or different from its original, but
nonetheless, the same.
Thank you to everybody who submitted a solution to this problem!

