Tables teaser
Problem
Have a look at this grid:
Can you see how it has been made?
Why is the 60 in that particular square?
Why does 20 appear twice?
In the interactivity below, some of the grid is filled in for you.
Can you work out which number goes in each row and column heading?
Once you know what each heading must be, drag the purple numbers to the appropriate spaces. When you think you have cracked it, click "Show the solution" to see if you are right.
Getting Started
Where might you start? Why?
Are there any row or column headings you know straightaway? Why?
How might that row/column heading help us now?
What do you know about numbers in the 10 times table?
What do you know about numbers in the 5 times table?
Student Solutions
Well done to everybody who got all of the grid headings correct! Lots of children sent us pictures of their finished grid, but only a few children explained their methods for completing it.
Bella from the British Vietnamese International School in Vietnam explained how the times table grid works:
How this table will work is the numbers on the row on the top will multiply with each number in the column in the left, for example if the first number on the the row is 4 and the first number on the column is 5 then take 4x5 and the answer is 20 then write 20 down in the grid under 4 and next to 5. Continue that with different numbers to finish the grid.
Well done, Bella - it's always a good idea to make sure that you understand how the grid works before trying to solve it.
Dhruv from Pict Model in India explained how he approached this problem:
First, I chose a random box and clicked on it. Then, when the number came I thought if it came in the table of 5 or 10. If a number came that was in the 5 times table I took the 5 digit and put it in the column and the row. If a number came that was in the 10 times table I will put a 10 digit in the row and the digit in the column that was in tens place in the number.
Thank you for sending us this explanation, Dhruv, and well done for looking at the numbers carefully to work out which times table they might be in. Will it always work if you put 10 as the row header and the other multiple as the column header?
Jil sent us a photo of her Tables Teaser grid, just before she clicked to show the solution:
Jil said:
I opened a few numbers. I then tried to understand what is common between those numbers (that are in the same column and row). I then understood that there is a pattern between the numbers in each row and column and placed the numbers according to those patterns.
Thank you for sending in this explanation! I wonder if Jil could have solved this by clicking on fewer than 10 squares?
Gia Han found all of the grid headings by only using 7 reveals:
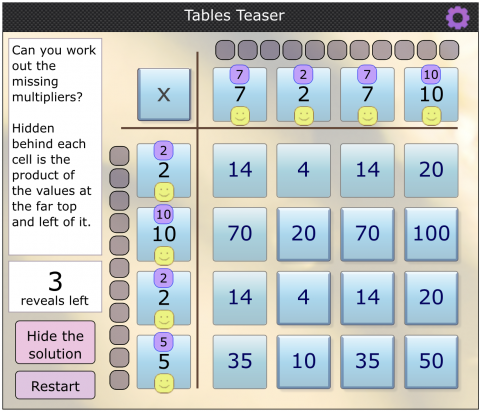
Well done! If you look closely, you can see that the numbers along the top and down the left-hand side have all been revealed. Skyler from Westridge also used this strategy:
You need to reveal all the numbers on the edge, that are next to the numbers you need to discover. Then you find the first multiples and work from there.
This is a good idea, Skyler. I wonder if you could choose to reveal all of the numbers along the bottom and down the right-hand side instead of the numbers next to the grid headings - would this strategy be different?
Jannah from ABQ Education Group in Oman also chose to reveal the numbers along the top and down the left-hand side, and she explained her reasoning in this video:
Good ideas, Jannah - I like how you looked carefully at which numbers could multiply together to give each of the numbers that you revealed.
Issa, Saja and Mohammed from ABQ Education Group in Oman each managed to solve the grid by only revealing six numbers, so they still had four reveals left at the end. I wonder what the smallest number of reveals possible is if you want to work out all of the grid headings without guessing... Would the smallest number of reveals change depending on the numbers you reveal in the grid?
Teachers' Resources
Tables Teaser
Have a look at this grid:
Can you see how it has been made?
Why is the 60 in that particular square?
Why does 20 appear twice?
In the interactivity below, some of the grid is filled in for you.
Can you work out which number goes in each row and column heading?
Once you know what each heading must be, drag the purple numbers to the appropriate spaces. When you think you have cracked it, click "Show the solution" to see if you are right.
Why do this problem?
The 'reverse' nature of this task (i.e. the fact that the answers to the multiplication calculations are given) will encourage children to be more curious about the mathematics, compared with being asked for answers to times tables questions. (This problem only uses the 2, 5 and 10 times tables, up to 12x.) In order to work out the row and column headings, learners will be mentally running through many tables facts or many calculations, and selecting those which could be applicable. The task requires children to make connections, notice patterns and apply their knowledge in a way that completing a list of times tables questions does not do.
Possible approach
This problem featured in an NRICH Primary webinar in April 2021.
Display the image of the completed three by three table square without saying anything by way of explanation and invite learners to consider what they see and what they notice. Give everyone chance to talk to a neighbour about their noticings and any questions that they might have before gathering as a whole group to share observations.
Facilitate discussion so that you are confident everyone understands the construction of a table square. You could then show the interactivity on the board and ask children what they notice this time. Establish the set-up so that learners know the challenge is to find the headings of the rows and columns, using the products given in the grid.
Give pairs time to talk to each other about where they might start and gradually fill in the headings as a whole group, ensuring that you demand clear reasoning from everyone.
Learners can then use the interactivity themselves in pairs, either at computers or using tablets. As they work, listen out for examples of high quality reasoning which you could then share in a plenary.
Use time at the end of the lesson to discuss which numbers are particularly helpful and why. (For example, 25 has to be 5x5.)
Key questions
Where might you start? Why?
Are there any row or column headings you know straightaway? Why?
How might that row/column heading help us now?
What do you know about numbers in the 10 times table?
What do you know about numbers in the 5 times table?
Possible support
If an adult is available to be with a few children who are struggling, they could suggest which cell to focus on first so that learners have some immediate success.
Possible extension
Mystery Matrix works in the same way, but any numbers from 2 to 12 are used to generate the products, so the answers will not just be multiples of 2, 5 and 10.