Swimming Pool Tiles
This activity creates an opportunity to explore all kinds of number-related patterns.
Problem

Most swimming pools are surrounded by tiles of some sort, like the pool in the photo above.
Imagine that we number the tiles around the pool.
In the image below, the pool takes up a 5 by 5 square and the space around the pool is five tiles wide:
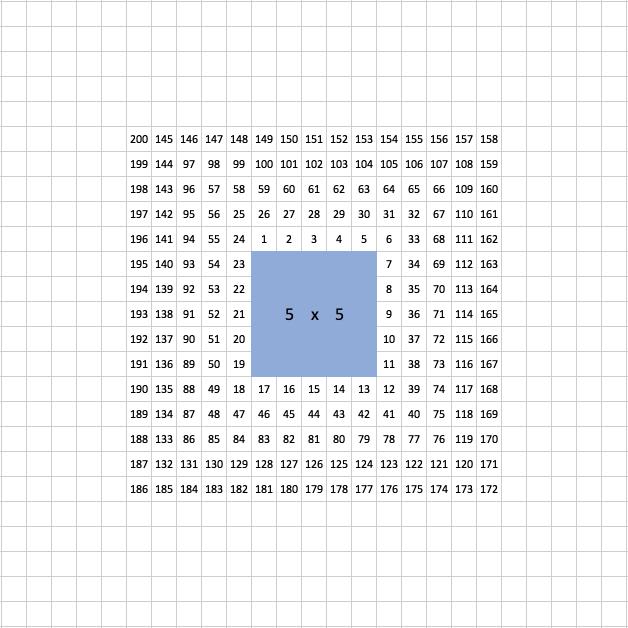
Can you describe how the tiles are numbered?
Think about a series of numbers that you know about, for example square numbers, prime numbers, triangle numbers...
Explore where those numbers occur in the path around the pool.
What do you notice?
What happens if you look at the path those numbers make around a different sized pool? (You may find it useful to print off this sheet which includes pools of different sizes up to 7 by 7.)
Please let us know what you discover!
Getting Started
These Word documents might be useful. They already mark square numbers/prime numbers/triangle numbers on different sized grids: SquareNumbers, PrimeNumbers, TriangularNumbers.
Student Solutions
Mr Garrod from Waverley Primary School wrote to share how his class had worked on this task:
We really enjoyed looking at this problem. The children observed a variety of patterns emerging from different number series. It was especially useful to highlight the difference between values. Here are their findings, as we recorded them as a class group:
- The number of tiles between square numbers increases by a difference of two each time (e.g. the tile difference between 1 and 4 is two blank tiles, between 4 and 9 is 4, between 9 and 16 is 6 tiles, and so on).
- Odd and even numbers create an alternating checked pattern.
- The diagonals in from 200 are all even; the diagonals in from 199 are all odd.
- Multiples of 4 create perfect patterns of diagonals across the tiled area.
- With prime numbers, there is an alternating difference of 1 and 3 tiles between each entry in the series (e.g. between 3 and 5 is one tile, between 5 and 7 is one tile, between 7 and 11 is three tiles, between 11 and 13 is one, 13 and 17 is three, 17 and 19 is one, etc).
- In the diagonal rows, there is an alternating pattern of units (e.g. from 191 to 153 diagonally: 1713317133)
- Triangular numbers give a steady incremental tile difference between each entry (1 tile difference, 2 tile difference, 3 tile difference, etc).
There is probably a lot more to find, but these became apparent after our first lesson. We put a series of the 100 squares provided onto large sheets of sugar paper and worked from this is groups.

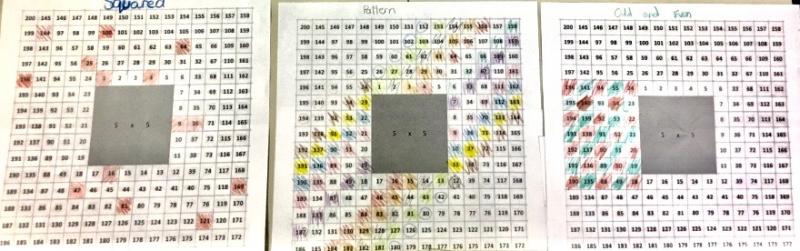
The above images may be viewed more clearly here and here.
Four pupils from Rowan Class at Stourport Primary Academy submitted their work:
Daisy
The following photos show some of the patterns I discovered when I tried the Swimming Pool Tiles problem. I couldn't see an obvious pattern to the 5 times table, but once I had highlighted all the numbers in the 3 times table I noticed that you could join these up in groups of three to make a pattern of rotating triangles.
After I had completed this I wondered why there was this obvious pattern of triangles with the 3 x table but no obvious pattern with the 5 x table. I wonder whether there would be a clearer pattern if I tried the 5 x table on a bigger grid.



Lois
I decided to colour all the multiples of 9 on the different sized grids. I noticed that if you join all the numbers with lines (so you would join 9 to 18, then 18 to 27 and so on), there is a pattern where it makes a spiral of shapes. It goes from a triangle to a square to a pentagon and so on so the shapes within the spiral increase by one corner each time. Here are the photos of my work to prove it! Originally I had made a prediction that odd-numbered times tables wouldn't have a pattern. I was wrong!
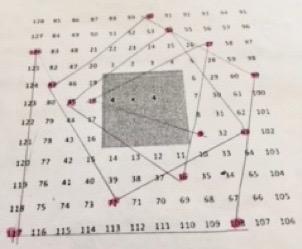

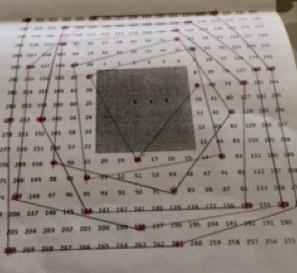
Keira
Most of my friends said that there isn't a pattern for the 5 x-table but I thought you could group the highlighted numbers together and make petals on a flower like this. My group had a go, with help from our teacher, at working out how you could predict how many tiles would be needed to go around different pool sizes. One of my friends spotted that if you multiply the area of the pool by 8 you get the number of tiles needed to go around it. For example, if the pool is 3 x 3 you would do 3x3=9 then multiply 9 by 8 which gives you 72 tiles. We checked this with all the tiles on the sheet and found this to be true. Then we used the same formula to calculate how many tiles would surround a pool that is 100 x 100.
100 x 100 = 10000. 10000 x 8 = 80000. We decided not to have a go at drawing that one!

Tom describes what he did:
I decided to investigate the 4 times table and discovered a diagonal pattern.
Next, I decided to colour the 4s, 8s and 12s on the same grid. Exactly the same numbers were coloured because of course the 8 and 12 times tables are also multiples of 4. I also spotted that if you join up the diagonal lines and join up the sides you make six isosceles trapeziums. This lesson was one of my favourites ever maths lessons.


These pieces of work are fantastic and suggest you were curious to find out more, as well as being resilient as you had a mathematical adventure. The work of the Stourport pupils and particularly their images can be more easily viewed here: All Stourport Swimming Pool Tiles.doc
Teachers' Resources
Why do this problem?
This activity is designed to nurture children's curiosity by introducing mathematics into a familiar non-mathematical context. Children might end up pursuing different ideas from each other and this freedom to explore may well encourage learners to persevere more than they might usually. In this way, they will immerse themselves in the particular number sequence they have chosen to use, which will help them gain a deep understanding of its structure. This activity lends itself to pupils posing their own questions in the form "I wonder what would happen if...?". (The further note at the foot of this page offers more support on curiosity in the classroom generally.)
Possible approach
You could display the picture of the numbered tiles around the 5 by 5 pool and simply say that it represents a swimming pool surrounded by square tiles. Ask learners to say what they see and use the ensuing discussion to draw out the key features of the picture.
Try not to say too much more at this stage and set learners off on the task of choosing a number sequence to explore on the numbered tiles. After some time, you could bring everyone together for a mini plenary to share some discoveries so far and to discuss ways of working and/or recording methods that are proving useful. As they are being driven by their own curiosity, encourage learners to share anything at all they have found/noticed. In addition, use the mini plenary to remind everyone that this is not just about pattern spotting, but they should try to explain and justify their 'noticings'.
Key questions
Tell me about what you're doing.
What do you notice?
Can you explain why that happens?
Possible extension
Encourage learners to pose their own questions along the lines of "I wonder what would happen if I...?" Here are some possible ideas to explore further:
- Walking along a straight path to the pool, adding up the numbers on the five tiles and exploring the totals for different paths.
- Walking around the pool travelling from tile to tile without getting wet and exploring the number sequences that result.
- Changing the size of the pool (this sheet contains pictures of pools up to 7 by 7)
- Investigating where the times tables numbers appear
Possible support
These Word documents might be helpful, which already mark square numbers/prime numbers/triangle numbers on different sized grids: SquareNumbers, PrimeNumbers, TriangularNumbers.
Further note
You may be interested in the following talks given by Professor Susan Engels, which focus on encouraging curiosity and are available on YouTube:
The Rise and Fall of Curiosity - the extract from 23.50 to 37.15 on adult encouragement and teacher behaviour is particularly worth viewing
The Hungry Mind: The Origins of Curiosity - the extract from 8.22 to 12.29 on children asking questions is especially useful.
