Squares in rectangles
A 2 by 3 rectangle contains 8 squares and a 3 by 4 rectangle contains 20 squares. What sizes of rectangle contain exactly 100 squares? Can you find them all?
Problem
Squares in Rectangles printable worksheet
A $2$ by $3$ rectangle contains $8$ squares. Can you see how?
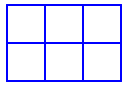
A $3$ by $4$ rectangle contains $20$ squares. Can you see how?

A $4$ by $6$ rectangle contains $50$ squares. Can you see how?

What size rectangle contains exactly $100$ squares?
Is there more than one?
Can you find them all?
Can you prove that there are no more?
Click here for a poster of this problem.
Getting Started
A $2$ by $3$ rectangle contains $8$ squares:
six small $1\times 1$ squares and two larger $2 \times 2$ squares

A $3$ by $4$ rectangle contains $20$ squares:
twelve $1\times1$ squares, six $2 \times 2$ squares and two $3 \times 3$ squares

Consider rectangles with a height of $2$ units.
Increase their width by $1$ unit at a time.
What effect does this have on the total number of squares?
Make a note of the number of squares in rectangles with a height of $2$ units.
Do you notice anything special?
Use your results to decide whether a rectangle with a height of $2$ units can contain exactly $100$ squares?
What about rectangles with a height of $3, 4, 5, \ldots$?
Draw up a table of results.
Student Solutions
Many people suggested the answer should be $6$ by $8$, because this is "double" the $6$ by $4$ example given in the problem. However, this doesn't take into account squares contained in the $6$ by $8$ rectangle which are not contained in the original $6$ by $4$ rectangle, like the red ones below:
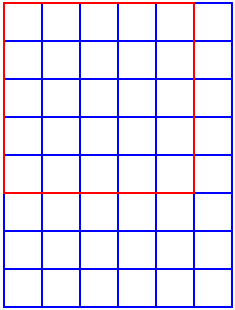
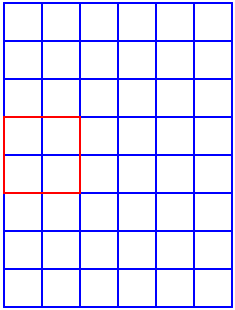
In the first picture, we have a $5 \times 5$ square. You cannot fit any of these in a $6 \times 4$ rectangle, but you can fit them in a $6 \times 8$ rectangle.
Imagine the $6 \times 8$ rectangle is made up from joining two $6 \times 4$ rectangles. In the second picture, you can see a $2 \times 2$ square. Where the $6 \times 4$ rectangles meet there will be an extra row of these $2 \times 2$ squares that would not be in either of the $6 \times 4$ rectangles.
columns: rows: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 2 | 5 | 8 | 11 | 14 | 17 | 20 |
| 3 | 3 | 8 | 14 | 20 | 26 | 32 | 38 |
| 4 | 4 | 11 | 20 | 30 | 40 | 50 | 60 |
| 5 | 5 | 14 | 26 | 40 | 55 | 70 | 85 |
| 6 | 6 | 17 | 32 | 50 | 70 | 91 | 112 |
| 7 | 7 | 20 | 38 | 60 | 85 | 112 | 140 |
Since the number of squares in an $n \times m$ rectangle is the same as the number of squares in an $m \times n$ rectangle, we will look only at rectangles with at least as many columns as rows. These are italicised in the above table.
First we notice that, if there is one row, increasing the number of columns by one increases the number of squares by $1$. This is because the only size of square that we can make is $1 \times 1$, so adding a column adds just one square.
If there are two rows, adding an extra column increases the number of squares by $3$. Why is this? Well, if we add an extra column we can make $2$ additional $1 \times 1$ squares and $1$ additional $2 \times 2$ square. This is a total of three extra squares. If we continue the pattern $2, 5, 8, \ldots$ in the $2$ row, we eventually get to $\ldots, 98, 101, \ldots$ - missing out $100$. This tells us that it isn't possible to make a rectangle with $100$ squares which has $2$ rows.
If there are three rows, adding an extra column allows us to make 3 more $1 \times 1$ squares, $2$ more $2 \times 2$ squares and $1$ more $3 \times 3$ square. This is a total of $6 = 3 + 2 + 1$ squares. This gives us the sequence $14, 20, 26, 32, \ldots, 98, 104, \ldots$ which tells us that we can't make a rectangle with exactly $100$ squares which has $3$ rows.
Using the same reasoning for four rows, we see adding a column increases the number of squares by $10$, and that we can make rectangles with $20, 30, \ldots, 90, 100, 110, \ldots$ squares. $100$ is in this list! In fact, a $4 \times 11$ rectangle contains exactly $100$ squares.
We can repeat this for the other rows in the table to find all the rectangles with exactly $100$ squares. These are $1 \times 100$, $4 \times 11$ and $5 \times 8$.
Mr Lunn's Year 7 class from The Wensleydale School reasoned in a very similar way. Here is a summary of their findings, showing a link between the results and Triangle Numbers.
Sandeep from Nrayana Junior College and Terence from Brumby Engineering College used a slightly different approach to count the number of squares in rectangles of different sizes, starting with the examples from the problem page. Here is Sandeep's method:
In a $2 \times 3$ rectangle, squares of side $1$ unit and squares of side $2$ units can be formed.
Number of squares of side $1$ unit is $2 \times 3 = 6$.
Number of squares of side $2$ units is $1 \times 2 = 2$.
Therefore the total number of squares in a $2 \times 3$ rectangle is $6 + 2 = 8$.
Similarly if we consider a $3 \times 4$ rectangle there are a total of $20$ squares.
Number of squares of side $1$ unit: $3 \times 4 = 12$.
Number of squares of side $2$ units: $2 \times 3 = (3-1) \times (4-1) = 6$.
Number of squares of side $3$ units: $1 \times 2 = (3-2) \times (4-2) = 2$.
Total number of squares $= 12 + 6 + 2 = 20$.
We can generalise this fact by taking a rectangle of $x$ rows and $y$ columns: $$\text{Total number of squares} = x \times y + (x-1) \times (y-1) + (x-2) \times (y-2) + \ldots$$ The addition series stops only when either the rows or the columns reduces to 1.
By trial and error, 5 $\times$ 8 and 4 $\times$ 11 rectangles contain exactly 100 squares. There can be no other rectangles containing 100 squares. This can be verified by increasing or decreasing the number of rows and columns.
Teachers' Resources
Why do this problem?
Possible approach
This printable worksheet may be useful: Squares in Rectangles.
Start by displaying the $20$ and $50$ diagram and asking how many squares there are. It may be appropriate to give the answers and then ask pairs to go to the front to explain - one to talk, and one to write/draw/record on the board. Well laid out number work will help with the algebra later, so the students' boardwork should prompt more suggestions about how to record working for this problem.
Present the problem, give students an opportunity to share first ideas. Several approaches (working backwards, trial and error, building up from smaller ones, systematic searching) might be suggested, and advantages/disadvantages discussed.
Encourage students to compare results with peers, and to resolve discrepancies without relying on the teacher's spreadsheet (see below). It might be useful to gather the results of the students as they work, to help them to see patterns and encourage them to conjecture what the results will be for other rectangles.
Key questions
How might you organise a search for rectangles with exactly $100$ squares?
Consider rectangles with a height of $2$ units, and increase their width by $1$ unit at a time.
What effect does this have on the total number of squares?
Can a rectangle with a height of $2$ units contain exactly $100$ squares?
What about rectangles with a height of $3, 4, 5, \ldots$?
Possible support
Struggling students could shade squares on Worksheet 1 and Worksheet 2 with lots of small copies of 3 by 4, 3 by 5 and 4 by 6 rectangles. Encourage them to work systematically, in order to observe the structure, and then make conjectures about the number of the next size of square, or in the next rectangle.
Encourage students to start by considering rectangles with a height of $2$ units, increase their width by $1$ unit at a time, and in a table, record the number of squares in different rectangles with a height of $2$ units.
Do they notice anything special?
Encourage them to use their results to decide whether a rectangle with a height of $2$ units can contain exactly $100$ squares.
What about rectangles with a height of $3, 4, 5, \ldots$?
Possible extension
Prove that you have all the rectangles.
