Skeleton shapes
How many balls of modelling clay and how many straws does it take to make these skeleton shapes?
Problem
Skeleton shapes are made with balls of modelling clay and straws.
This shows a cube and a skeleton cube:
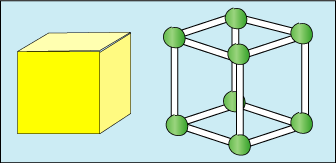
How many balls of modelling clay and how many straws does it take to make the cube?
Here are some piles of modelling clay balls and straws:
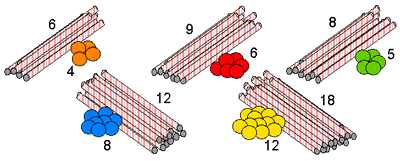
For accessibility: 5 piles of modelling clay balls and straws. The first pile has 6 straws and 4 balls of modelling clay. The second pile has 9 straws and 6 balls of modelling clay. The third pile has 8 straws and 5 balls of modelling clay. The fourth pile has 12 straws and 8 balls of modelling clay. The fifth pile has 18 straws and 12 balls of modelling clay.
Look at the shapes below and decide which piles are needed to make a skeleton of each shape.
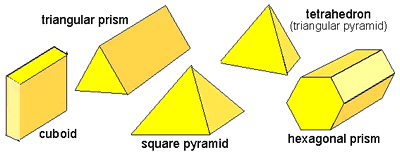
How do you know which piles go with which shape?
Getting Started
It might help to use real shapes so that you can count the number of edges and vertices (corners) they have.
How many edges does the first shape have? So how many straws would be needed?
How many vertices does it have? So how many balls of modelling clay would we need to make it?
Student Solutions
We had lots of correct solutions to this problem and you used many different ways of helping yourselves to reach the answers. Some of you made the shapes from straws and modelling clay, like Rachel, Abigail and Alistair from Histon and Impington Infant School. They sent in a photo of their models:
Others of you decided to make the shapes from Polydron, while some of you drew the shapes carefully. Alice from Tattingstone, and Scarlett and Sam from Cupernham, were among those who opted for drawing, but William, also from Cupernham sent in particularly careful sketches using isometric paper:
Cuboid : 8 balls, 12 straws
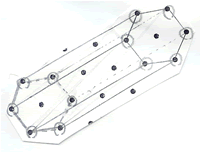
Hexagonal prism : 12 balls, 18 straws
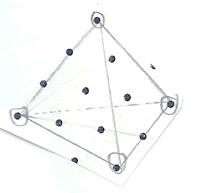
Square pyramid : 5 balls, 8 straws
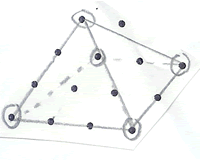
Tetrahedron : 4 balls, 6 straws
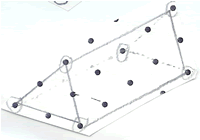
Triangular prism : 6 balls, 9 straws
Chris and Michael from Moorfield Junior School also sent some excellent drawings and took the problem a step further by looking at the relationship between the number of faces, edges and vertices of different prisms. They enclosed this table:
| Type of prism | Faces | Vertices | Edges |
|---|---|---|---|
| triangular | 5 | 6 | 9 |
| cube or cuboid | 6 | 8 | 12 |
| pentagonal | 7 | 10 | 15 |
| hexagonal | 8 | 12 | 18 |
| heptagonal | 9 | 14 | 21 |
| octagonal | 10 | 16 | 24 |
| nonagonal | 11 | 18 | 27 |
| decagonal | 12 | 20 | 30 |
Chris and Michael say:
There are patterns you can see in the vertices and edges columns. The number of vertices is double the amount of sides on the 2D shape at each end. In the edges column it's three times the amount of sides on the 2D shape.
Perhaps you can spot some more patterns too. Let us know if so.
Thank you also to these people who sent us correct answers too:
Hugo, Emile and Benny from Wesley College Prahran Preparatory School in Melbourne, Australia.
Charlotte and Thomas.
Al from Dudley.
Ryo, Jake and Charlie from Moorfield Junior School.
Samuel from Bispham Drive Junior School in Nottingham.
David from Tithe Barn Primary School.
Teachers' Resources
Skeleton Shapes
Skeleton shapes are made with balls of modelling clay and straws.
This shows a cube and a skeleton cube:
How many balls of modelling clay and how many straws does it take to make the cube?
Here are some piles of modelling clay balls and straws:
Look at the shapes below and decide which piles are needed to make a skeleton of each shape.
How do you know which piles go with which shape?
Why do this problem?
This problem helps children begin to become familiar with the various properties of common geometric solid shapes, concentrating on edges and vertices. It also helps in promoting discussion and experimentation. Naming the shapes should be a help during discussion and description of what has been done, rather than being an exercise in its own right.
Possible approach
Before doing this problem children should have had plenty of free play building with sets of solid shapes so that they begin to get a feel for their properties. They should also have chance to experiment with building skeleton shapes either with a specific kit or with drinking straws and modelling clay/plasticine.
Key questions
How many edges did you count? What does this tell you about the number of straws we need?
How many corners did you count? What does this tell you about the number of balls of modelling clay we need?
How many edges meet at this corner?
Possible extension
Possible support
Start by counting the faces on a cube - a large dice might be useful - and then the edges and finally the vertices. A non-permanent pen could be used to mark a real shape if children are having difficulty keeping track of their counting.