Shape products
These eleven shapes each stand for a different number. Can you use the multiplication sums to work out what they are?
Problem
Shape Products printable worksheet
Shape Products printable worksheet - extra clues
The coloured shapes stand for eleven of the numbers from $0$ to $12$. Each shape is a different number.
Can you work out what they are from the multiplications below?
A Image
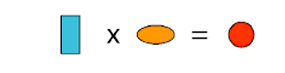
| B Image
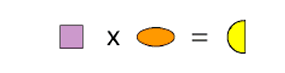
|
C Image
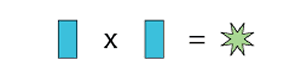
| D Image
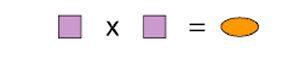
|
E Image

| F Image

|
G Image

| H Image

|
If you need some more clues, click below to reveal four more multiplications:
I Image
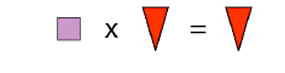
| J Image

|
K Image

| L Image

|
Extension
Once you have worked out the value of each shape above, take a look at the two multiplications below:


Can you work out the value of the shapes in each product?
This activity originally featured in the hands-on Brain Buster Maths Boxes, developed by members of the NRICH Team and produced by BEAM. These resources are out of print but can still be found on Amazon.
Getting Started
Charlie noticed that B, D, E and G all contain a purple square.
Alison noticed that F and H both had a shape that appeared in the product and the answer.
Becky noticed that the answer to D was part of the product in B.
Can you use any of their ideas to help you to deduce any of the shapes?
Student Solutions
Thank you to everyone who sent in a solution. There were too many good solutions to mention everybody here, but this is a selection of what we received.
Jessica from Royds School in the UK used a trial approach to solve the problem:
We started trying numbers for the blue rectangle. We found that 3 worked and then we used this to fill the rest of the numbers. We wrote a list a list of the numbers at the top of the page to see which we had used.
Siri and Amelie from Priestlands School in the UK used a systematic method to make sense of the equations. They said:
We used a trial and error technique to find out which shapes were what - by writing out the numbers 0 to 12 by each shape, we were able to cross out the numbers which we knew were impossible for our shape to be, eventually leaving us with the answer.
Anny from St Mary's School, Cambridge in the UK sent in this solution, using factors to find the values of the shapes.

Abi from The Grange School, William from Methodist College and Tia from North London Collegiate School, all in the UK, began by looking at the equations which involved squaring. Abi said:
I first noticed that the products of equations C and D are both square numbers. Since the products of both are different to the factors, this rules out 1 and so there are only two possible square numbers between 0 and 12: 4 and 9. Therefore the oval and the star each equal 4 or 9, and the rectangle and the square each equal 2 or 3.
Equation B involves the two different integers from equation D. The two possible answers must be [2 $\times$ 4 = 8] or [3 $\times$ 9 = 27]. 27 isn't a number between 0 and 12, so this can't be the correct equation. Instead, we know that the purple square is equal to 2, the orange oval is equal to 4, and the yellow semicircle is equal to 8. This also means that equation C is [3 $\times$ 3 = 9]. We can substitute these numbers into other equations A,E,F,G.
Equations F and H have the same product as one of its factors. This means that one of the factors in each equation has to be either 1 or 0. In equation F, we know that [a $\times$ 8 = a]. The red triangles (a) have to be 0 because anything multiplied by 0 is 0. I also know that it can't be 1 as [1 $\times$ 8 = 8]. These numbers are the wrong way round for this equation to work. 1 must therefore fit in equation H as the yellow diamond.
As I have substituted some shapes in the equations for numbers I already know, equation A is left as [3 $\times$ 4 = a]. a (or the red circle) is easy to find to be 12. 12 is also the solution to equation E: [a $\times$ 2 = 12]. By making a the subject, we know that [a = 12/2 = 6].
We are now left with unknown numbers in only equations G and H. G says [2 $\times$ a = c]. This means that c is an even number. The numbers remaining to choose from are 5,7,10 and 11, of which 10 is the only even number. This is the blue hexagon. By changing equation G to make the purple star the subject, we know that [a = 10/2 = 5].
Vid from Primary school Loka ÄŒrnomelj in Slovenia sent in a very clear solution which uses a mixture of the two methods above. You can see Vid's solution here: vid.pdf
Sophie, Amelia and Natasha from Holy Trinity CE Academy, Rothwell in the UK sent in their work on the extension. This is how they solved the problem:
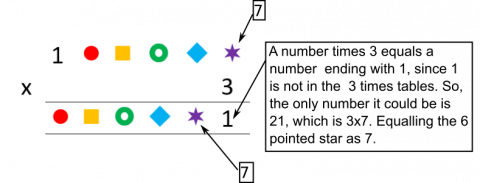
After figuring out the first number, we decided to work our way along the line of shapes.

After figuring out how to work out each shape's number, these were our answers:

Teachers' Resources
Why do this problem?
Possible approach
These printable resources may be useful: Shape Products
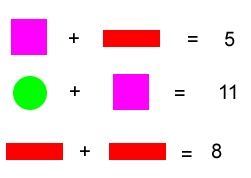
Key questions
What is unusual about clues F and H?
Possible extension
Possible support
It may be appropriate for some students to start this activity with the Support worksheet with all 12 clues. Some students may like to cut out the 12 clues and move them around in order to more easily compare pairs that contain the same shape.
