Shady symmetry
How many different symmetrical shapes can you make by shading triangles or squares?
Problem
Shady Symmetry printable sheet - problem
Shady Symmetry downloadable slides - images
Printable square grid template
Printable isometric grid template
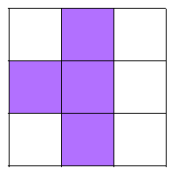
Charlie created a symmetrical pattern by shading in four squares on a 3 by 3 square grid:
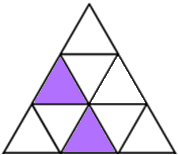
Alison created a symmetrical pattern by shading in two triangles on a 3 by 3 isometric grid:
- How many different patterns can you make if you are only allowed to shade in one... two... three... four cells?
- How does the number of patterns with 6 cells shaded relate to the number with 3 cells shaded?
- Can you make patterns with exactly one... two... three... four lines of symmetry?
- Can you make patterns with rotational symmetry AND lines of symmetry?
- Can you make patterns with rotational symmetry but NO lines of symmetry?
- Can you make patterns using more than one colour?
Getting Started
Begin by looking at all the patterns that can be made by colouring in just 1 cell, then 2, then 3, and so on...
Student Solutions
There are many possible questions to think about in this problem. A systematic approach is important to avoid counting the same patterns twice, or missing any out!
Melissa, Damien, Katy, Saskia, Lauren, Maria, Tanvi, Raffie, Sophie and Charlotte looked at the isometric grids, counting patterns with different numbers of shaded little triangles.
It's important to decide what a different pattern means, for example if you shade the top little triangle at the vertex, and the left-most little triangle at the left vertex, are these different patterns? Damien considered these as the same since they differ only by rotating the picture, but Melissa, Katy, Saskia, Lauren, Maria, Tanvi, Raffie, Sophie and Charlotte considered these as different.
Shading 1 little triangle: No matter which you shade there is exactly one line of reflective symmetry. That gives 9 patterns, or only 3 according to Damien, because any other can be rotated to look like one of these:
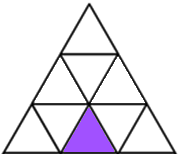
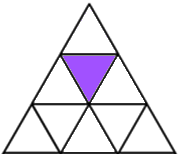
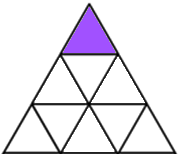
9 or 3 ways with 1 triangle shaded.
Shading 2 little triangles: To get a line of symmetry you need to choose carefully. To avoid counting patterns which look the same after a rotation we'll just look at the vertical line of symmetry. You can choose two of the triangles on the vertical line in the middle (three ways to do this) or one of the left-hand triangles with it's partner on the right (also three ways to do this).
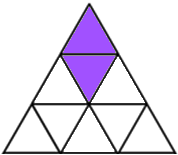
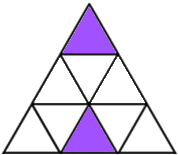
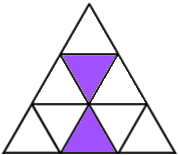
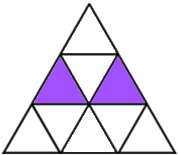
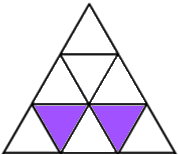
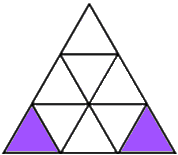
That gives 6 ways according to Damien, or 18 ways according to Melissa, Katy, Saskia, Lauren, Maria, Tanvi, Raffie, Sophie and Charlotte, since each pattern can be rotated to give 3 'different' ways.
Shading 3 little triangles: Raffie's diagram below shows the ways of making symmetrical shapes with 3 triangles shaded. Raffie includes rotations of the patterns as different patterns, so most of them are counted 3 times. Notice that the patterns which have rotational symmetry are not reapeated.
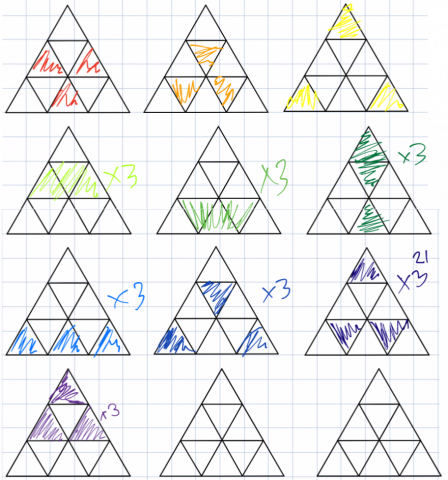
This gives a total of 7$\times$3 + 3 = 24 ways with 3 triangles shaded, or 10 ways if rotations are considered the same.
Shading 4 little triangles: This is Sophie and Charlotte's diagram showing the symmetrical patterns using 4 tiangles.
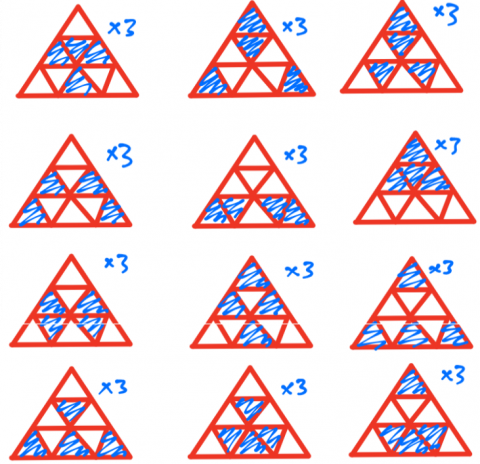
All of them are multiplied by 3 because Sophie and Charlotte counted rotations as different patterns, which gave them a total of 36.
Counting rotations ass the same pattern, there are only 12 symmetrical patterns with 4 little triangles shaded.
Shading more little triangles: Katy, Saskia, Lauren, Maria, Tanvi, Raffie, Sophie and Charlotte continued, and drew tables showing how many symmetrical patterns there are for different numbers of triangles.
| Number Shaded | Number Made |
| 0 | 1 |
| 1 | 9 |
| 2 | 18 |
| 3 | 24 |
| 4 | 6 |
| 5 | 36 |
| 6 | 24 |
| 7 | 18 |
| 8 | 9 |
| 9 | 1 |
They noticed that the last one matched with the first one, the second last one matched with the second one and so on. There is a reason for this:
Imagine for example that 2 triangles are shaded in a symmetrical pattern. Then since the whole shape is symmetrical, the 7 triangles that are not shaded must also be in a symmetrical pattern. Look at the patterns that are left white in the pictures above!
More lines of symmetry: Notice that the patterns with 1 and 2 shaded triangles always have only 1 line of symmetry. Some of the patterns with 3 shaded triangles have 3 lines of symmetry and rotational symmetry.
Can you find any patterns with exactly 2 lines of symmetry? If so, how? If not, why not?
Christian investigated the square grid and found many patterns like the ones below. Notice that we can use a similar method for finding patterns exploiting symmetry. Things seem a bit more complicated with the square though...
Shading 1 little square: The square has two distinct types of reflectional symmetry; in diagonal and in side-bisecting lines. No amount of rotating the square makes these symmetries look the same. Like with the isometric grid, there are 3 ways of shading 1 square:

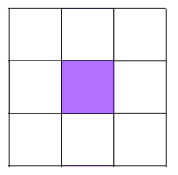
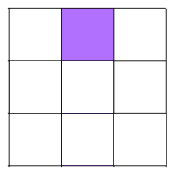
Shading 2 little squares: We'll need to shade two squares along a line of symmetry or a pair either side of a line of symmetry. Remember the diagonal and the side-bisecting lines! Be careful not to double count some patterns because opposite corners can be made to look the same by 180 degree rotations!
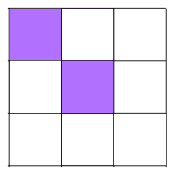
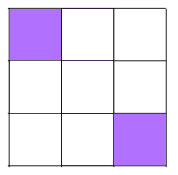
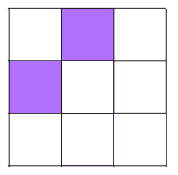
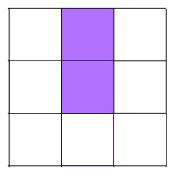
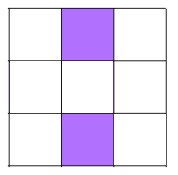
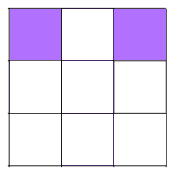
There are 6 different patterns with 2 shaded squares.
Shading 3 little squares: Use the same method as before - work systematically along and either side of lines of symmetry.
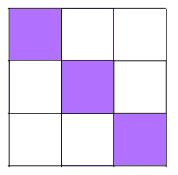
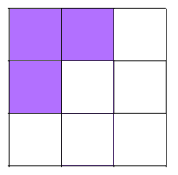
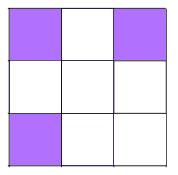
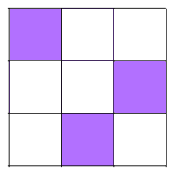
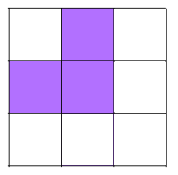
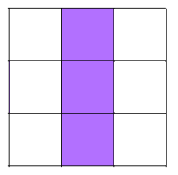
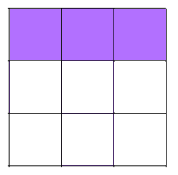
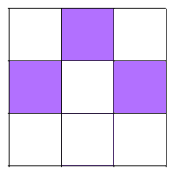
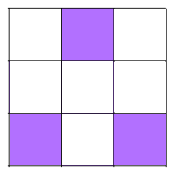
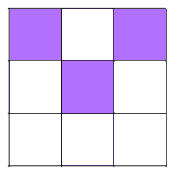
There are 10 different patterns with 3 shaded squares.
Do you notice anything similar to the isometric case? What about 4, 5, 6, 7 or 8 shaded squares? Do you need to do any more work?
There are many more questions that you could ask about these patterns. Have fun investigating further.
Teachers' Resources
Why do this problem?
This problem provides an engaging challenge that requires students to work systematically at producing various symmetrical patterns. There are a variety of avenues for exploration and extension work, and learners' results can be used to brighten up the classroom walls.
Possible approach
These printable resources may be useful: Shady Symmetry problem,
Shady Symmetry images,
Shady Symmetry Isometric Template,
Start by displaying the two patterns from the problem for everyone to see - they are available on this PowerPoint Slide.


Ask students to discuss the two images in pairs, focusing on what they notice about the two pictures, what is the same and what is different. Then bring the class together to share their ideas.
Key questions
- What different types of symmetry do the initial grids exhibit?
- If you colour a triangle or square here, what else must be coloured in to keep it symmetrical?
- What are the possible symmetries of a finished pattern?
- How can you be sure you have found all the symmetric patterns?
Possible support
Encourage students to begin by looking at all the patterns that can be made by colouring in just 1 cell, then 2, then 3, and so on...
Possible extension
The problem can be extended to be done on these 4 by 4 square and triangular grids, and of course there are opportunities to extend into three dimensions...
