Set Square
A triangle PQR, right angled at P, slides on a horizontal floor
with Q and R in contact with perpendicular walls. What is the locus
of P?
Age
16 to 18
Challenge level
A triangle PQR, right angled at P, slides on a horizontal floor
with Q and R in contact with perpendicular walls. What is the locus
of P?
You might look for a cyclic quadrilateral.
We have constructed this in geogebra to help
Created with GeoGebra
NOTES AND BACKGROUND
You might like to download your own free copy of GeoGebra from the link above and draw this dynamic diagram for yourself. You will find it easy to get started on GeoGebra with the Quickstart guide for beginners.
The locus of the point $P$ is a straight line as the vertices $Q$ and $R$ slide along the walls.
Image
|
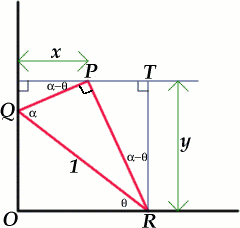
Sue Liu of Madras
College, St Andrew's sent this solution to the problem. Without
loss of generality we can let the length of $QR$ be 1 unit, and
take a coordinate system with the origin at $O$ and axes along $OR$
and $OQ$.
If $\angle PQR = \alpha$, where $0 < \alpha < 90^\circ$,
then $PQ = \cos \alpha$ and $PR = \sin \alpha.$ Let $\angle QRO =
\theta $ where $0 \leq \theta \leq 90^\circ$. Then, from the right
angled triangles $PSQ$ and $PTR$, we have $\angle PRT = \angle QPS
= \alpha - \theta$, and hence we can write down the coordinates of
the point $P$.
|
\begin{eqnarray} x &=& \cos \alpha \cos
(\alpha - \theta) \\ y &=& \sin \alpha \cos (\alpha -
\theta). \end{eqnarray}
We see that $${y\over x}= {\sin \alpha \cos (\alpha -
\theta)\over \cos \alpha \cos (\alpha - \theta)}= \tan \alpha.$$
and so $P$ lies on the straight line $y = x\tan \alpha$.
The position $(x,y)$ depends only on $cos(\alpha - \theta)$,
$\alpha$ being a constant, and $\theta$ a variable. The distance of
the point $P$ from $O$ is given by $$OP^2 = x^2 + y^2 =
\cos^2(\alpha - \theta)(\cos^2\alpha + \sin^2\alpha) =
\cos^2(\alpha - \theta).$$ Hence $OP = \cos(\alpha - \theta)$ which
is a maximum when $\cos(\alpha - \theta) = 1$, that is when $\alpha
= \theta$. This occurs when $OQPR$ is a rectangle as shown in the
diagram.
Image
We get an even simpler method of solution by using the fact that the angles $QOR$ and $QPR$ are both 90 degrees so that $OQPR$ is a cyclic quadrilateral with $PR$ as a chord. We have $\angle POR = \angle PQR = \alpha$ because these two angles are subtended by the same chord of the circle. This shows that $\angle POR$ is constant and hence that the locus of $P$ is the straight line $y = x \tan \alpha.$
What can you say about the locus of $P$ if the triangle $PQR$ is not a right angled triangle?