Semicircular Design
Weekly Problem 9 - 2016
The diagram to the right shows a logo made from semi-circular arcs. What fraction of the logo is shaded?
The diagram to the right shows a logo made from semi-circular arcs. What fraction of the logo is shaded?
Problem
Image
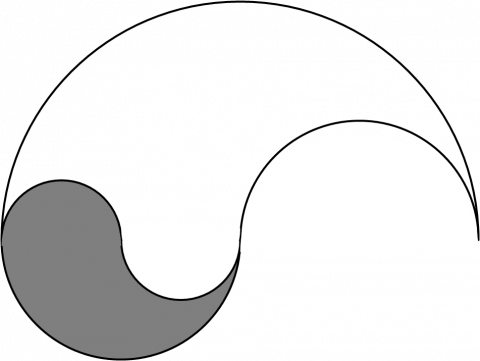
The diagram to the right shows a logo made from semi-circular arcs, each with a radius of $2$cm, $4$cm or $8$cm.
What fraction of the logo is shaded?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Answer: $\frac14$
Using areas of semicircles
Shaded part:
Image

Image
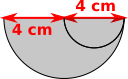
Semicircle radius $4$ cm has area $\frac12\pi\times4^2 = 8\pi$ cm$^2$
Whole design:
Image
Image
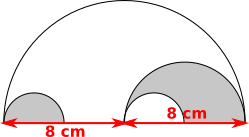
Semicircle radius $8$ cm has area $\frac12\pi\times8^2 = 32\pi$ cm$^2$
$\frac{8\pi}{32\pi} = \frac{1}{4}$ of the shape is shaded.
Using scale factors
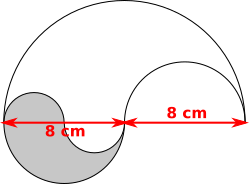
Shaded part:
Image

Image

Whole design:
Image
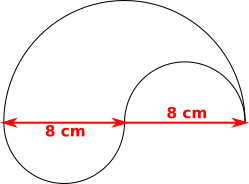
Shaded part is similar to whole design, length scale factor 2
Length scale factor 2 $\Rightarrow$ area scale factor 4
$\frac14$ of the shape is shaded
