Semicircle in a Semicircle
Problem
The diagram shows two semicircular arcs, PQRS and QOR . The diameters, PS and QR , of the two semicircles are parallel; PS is of length 4 and is a tangent to semicircular arc QOR .
What is the area of the shaded region?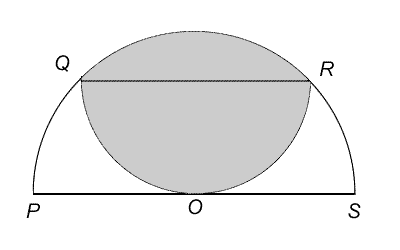
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Let T be the centre of the semicircle with diameter QR and let OT produced meet the circumference of the larger semicircle at U .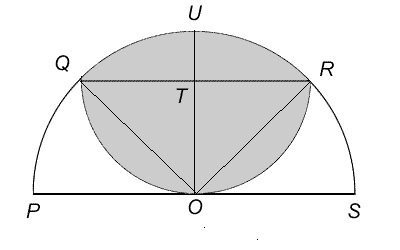
By symmetry, we note that OT is perpendicular to QR . As TR = TO = TQ (radii of the same semicircle), triangles ORT and OQT are both isosceles, right-angled triangles. So QOR is a right angle.
By Pythagoras' Theorem: QR ² = OQ ² + OR ² = 2 ² + 2 ² = 8. So $QR = \sqrt8$ = $2\sqrt2$ and the radius of semicircle QOR is $\sqrt2$.
