Rots and refs
Problem
The point $P$ has coordinates $(r\cos \phi, r\sin \phi)$ where the distance of $P$ from the origin is $OP=r$ and the line $OP$ is at angle $\phi$ to the x axis. Find the image of this point under the transformation given by the matrix
Draw a diagram and describe the effect of this transformation on the points of the plane.
The point $P$ has coordinates $(p,q)$ and the point $P'$ is the reflection of $P$ in the line $y = x\tan\theta$. In the diagram below the lines $P'X'$ and $XA'$ are perpendicular to the line $OA'X'$. "
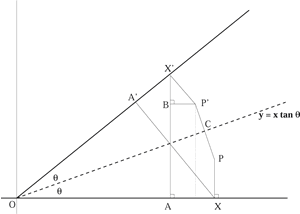
Prove that $OX = OX' = p$, $P'X' = PX = q$ and $OA = OA' = p\cos 2\theta.$ Find the lengths $BP',\ AX'$ and $BX'$ and hence prove that transformation given by the matrix
gives a reflection in the line $y=\tan\theta$.
Getting Started
See the problem 'The Matrix' for an explanation of how a transformation of the plane is given by a matrix and how you can find the image of a point by multiplying its vector by the matrix of the transformation.
Student Solutions
Bob sent us his solution:
Firstly I multiplied the matricies to find the new point. Using the trigonometric identities to simplify, I got the new point as $(r\cos(\theta+\phi),r\sin(\theta+\phi))$. This meant that we had rotated the point $\phi$ degrees anticlockwise.
To prove that $OX = OX' = p$, I drew a line XX', which intersects and is parallel to the line $y=x\tan\theta$ (call this point of intersection D). But $DX'=DX$ and so $ODX$ and $ODX'$ are two right-angled triangles of the same size, so $OX=OX'=p$. By the same argument I drew lines $OP$ and $OP'$, and so got right-angled triangles again, so $OP=OP'=q$.
By looking at the right-angled triangle $OAX'$, with the angle at $O$ being $2\theta$, I knew that: $$\cos2\theta=\frac{OA'}{OX}=\frac{OA'}{p}$$ and so $OA'=p\cos2\theta$.
I then looked at the right-angled triangle $X'BP$, and since the angle at $X$ is $2\theta$, $BP'=q\sin2\theta$. By applying Pythagoras' Theorem to the right-angled triangle $OAX$,$AX'=p\sin2\theta$. Finally, applying Pythagoras' Thereom to the triangle $X'BP'$ I found $BX'=q\cos2\theta$.
Looking at the change in X co-ordinates, I found $P'=(p\cos2\theta+q\sin2\theta, \; p\sin2\theta-q\cos2\theta)$.
So the matrix for the reflection would be:
