Rollin' Rollin' Rollin'
Two circles of equal radius touch at P. One circle is fixed whilst the other moves, rolling without slipping, all the way round. How many times does the moving coin revolve before returning to P?
Age
11 to 14
Challenge level
Problem
Two circles of equal radius touch at the point P. One circle is fixed whilst the other moves, rolling without slipping, all the way round.
How many times does the moving coin revolve before returning to P?
What happens if the radius of the moving circle is half that of the fixed circle? Can you generalise your results further?
Image
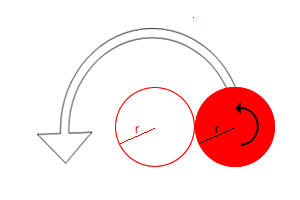
You may wish to use the GeoGebra interactivity below to test out your conjectures.
Here are two related problems you might like to take a look at:
Rolling Around
Is There a Theorem?
Getting Started
Use two coins to see what happens.
Image
How much has the moving coin turned when it is half way around the fixed coin?
You could consider how far the centre of the moving circle travels.
Student Solutions
Simon sent us this solution :
The obvious answer is that the outer circle (B say) rotating around the stationary circle (A) revolves once but this is wrong. Looking at the interactivity I could see that the mark on the circumference started on the left of the outer circle and was on the left again when the outer circle had only gone half way around. This means that it must make two full turns as it rotates around the inner circle. Now I need to explain why.
Let's start with each of the circles having a radius r. I thought about the centre of the outer circle. When it makes a full circuit of the inner circle the centre of the outer circle will have drawn a circle of raduis 2r so it will have covered a distance of $2 \pi \times 2r = 4 \pi r$.
So how many rotations has this outer circle made?
I next imagined the circle rolling along a line. How many revolutions would be necessary for the centre to travel the distance of $4\pi r$
In one revolution the centre will travel the same distance as the circle (imagine a bicycle wheel) that is a distance of $2\pi r$. So to travel a distance $4\pi r$ the circle would need to revolve twice. This means the outer circle makes two full turns for every single circuit of the inner circle.
Kevin of Langley Grammer School explained
what was happening for circles with different, as well as the same
radii.
The centre of the moving circle moves round the circumference
of a circle of radius $2r$, i.e. a distance $4\pi r$.
The centre of the moving circle moves a distance $2 \pi r$
when it makes one complete turn about its centre. Therefore when
the moving circle returns to $P$ it has made 2 complete
turns.
In this situation the ratio of the radii of the moving circle
to the non-moving circle was 1.
Let the non-moving circle have a radius of $r$, and the moving
circle have a radius of $nr$, so that the ratio of the radii is
$n$.
Therefore the centre of the moving circle moves along the
circumference of a circle with radius $(1+n)r$, i.e. a distance $2
\pi (1+n)r$. Therefore when the moving circle returns to $P$ it
will have made $$\frac{2\pi(1+n)r}{2 \pi nr} = 1+ \frac{1}{n}$$
turns. Therefore if the moving circle has a greater radius than the
non-moving circle then $n> 1$, and so $1/n$ would be less than
1, and so the number of turns would be less than 2. If the moving
circle has a smaller radius than the non-moving circle then $n<
1$, and so $1/n$ would be greater than 1, meaning that the number
of turns would be greater than 2.
It can also be seen that the moving coin makes at least 1
turn, regardless of the sizes of the circles, as 1/n is always
positive.
So, if the moving circle is half the radius of the inner circle it will turn $1+2 = 3$ times
If the moving circle is one third the radius of the inner circle - it will turn $1+3 = 4$ times.
Surprised?
Teachers' Resources
Why do this problem?
This problem is interesting because the answer is not at all obvious and will challenge students' perceptions. It is a great problem in visualisation and translating a visual concept into numbers or algebra.Possible approach
Start with the problem of two disks of the same size, one rolling around the other.
Discuss the problem and canvass the class for their instinctive response: how many revolutions will the first disk make? Ask them to go off and justify this response. Those who incorrectly assume that the disk turns one time will either become aware of their error or produce a faulty justification of their result.
The class could then discuss their result and give their explanations (faulty or otherwise). Choose two students with different results to present their ideas. Who convinces the rest of the class? [note: if the whole class is correct, then who can give the clearest explanation? If the whole class is incorrect then watch the animation and ask at what point the rolling disk is in the same
orientation as at the start]
Even when the correct answer has been worked out, students are likely to want to demonstrate this with physical objects such as a pair of coins.
The activity contains many extensions which are likely to become accessible once the initial problem is grasped.
Key questions
- How far does the centre of the rolling disk travel?
- Can you visualise the locus of a point on the edge of the rolling disk?