Roaming Rhombus
We have four rods of equal lengths hinged at their endpoints to
form a rhombus ABCD. Keeping AB fixed we allow CD to take all
possible positions in the plane. What is the locus (or path) of the
point D?
Age
14 to 16
Challenge level
Four rods of equal lengths are hinged at their endpoints to form a rhombus ABCD.
Image
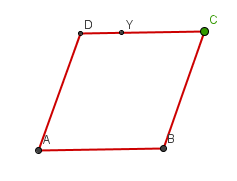
Keeping AB fixed, CD is free to move in the plane with the angle BAD between 0 and 180 degrees.
What is the locus (or path) of the point D?
What is the locus of Y, the point one third of the way along DC? (DY:YC = 1:2)
Well done Luke and Daniel from year 9 together with Nicholas and Luke from year 7 of Clevedon Community School who sent in the following solution.
The locus of corner D will be a circle with a radius equal to AD, whose centre is A. The locus of the point Y will be a circle with a radius equal to AD, and a centre on AB one third of the way along from A to B.
Can you see the reason for this? The locus of Y is a circle. If you imagine a line joining Y to the centre Z of this circle then DYZA is a parallelogram so ZY = AD and AZ=DY.