On the road

This solution was sent in by Ben at Madras College in St Andrews. Another good solution was sent in by Nicola at Madras College.

The car overtakes the scooter at 12.00. This point can be taken as the origin of a graph of distance against time.

Image

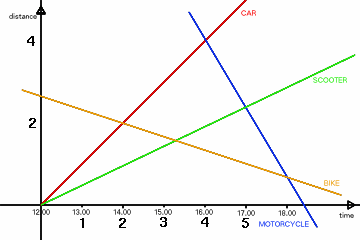
Assuming that the car travels at 1 unit per hour, the car therefore has equation y=x.

Now assume that the scooter travels at $a$ times the speed of the car, where $0 < a < 1$. So, it has equation $y=ax$.

Now for the motorcycle, whose line goes through $(4,4)$ and $(5,5a)$.

Gradient $= (5a-4)/(5-4) = 5a-4$

Substituting in the point $(5,5a)$,

$$ \begin{eqnarray} y - b &=& m(x-a) \\ y - 5a &=& (5a-4)(x-5) \\ y &=& 5ax - 4x - 20a + 20 \end{eqnarray} $$

To find the intersection of the motorcycle and bike, we know that $x=6$.

Therefore $y-5a = (5a-4) \times 1$, and so $y = 10a-4$.

For the bike,

$$ gradient = \frac{10a-4-2}{6-2} = \frac{10a-6}{4} $$

Using $(6, 10a-4)$, [Why not $(2,2)$? - Ed]

$$ \begin{eqnarray} y -b &=& m(x-a) \\ y - (10a-4)& =& \frac{10a-6}{4}(x-6) \\ 4y - 40a + 16 &=& 10ax - 6x - 60a + 36 \\ 4y &=& 10ax - 6x - 20a + 20 \\ \end{eqnarray} $$

When the bike meets the scooter, $y=ax$, so $4y=4ax$.

Therefore

$$ \begin{eqnarray} 10ax - 6x - 20a + 20 &=& 4ax \\ 6ax - 6x &=& 20a - 20 \\ 3ax - 3x &=& 10a - 10 \\ 3x(a-1) &=& 10(a-1) \\ 3x &=& 10 \\ x &=& 3\frac{1}{3} \end{eqnarray} $$

So, whatever the value of $a$, the scooter and bike meet 3 hours and 20 minutes after 12.00, at 15.20.