Real-life equations
Problem
This is a list of many of the most important equations in science. In each case, we have labelled the two variable quantities $x$ and $y$. The letters $a, b$ stand for constants in each case
Constant motion $\quad\quad\quad\quad\quad a = \frac{x}{y}$
Constant acceleration $\quad\quad\quad x = uy + \frac{1}{2} ay^2$
Beer Lambert Law $\quad\quad\quad\quad a=bxy$
Exponential decay $\quad\quad\quad\quad x=a e^{by}$
Michaelis-Menton $\quad\quad\quad\quad x = \frac{ay}{b+y}$
pH $\quad\quad\quad\quad\quad\quad\quad\quad\quad x = -\log_{10}(y)$
Can you identify the possible meanings of the variables $x$ and $y$ and the constants in each case?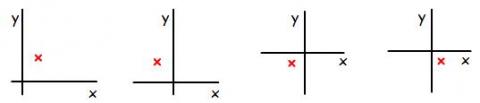
Four graphs are shown above, where the two axes intersect at the origin $(0, 0)$.
The red crosses show four measurements. Although we do not know the numerical values (because there are no scales on the graphs), we can see whether the values are positive or negative in each variable. For example, the first measurement is positive in $x$ and positive in $y$; the second measurement is positive in $y$, negative in $x$.
For processes evolving according to each of the equations above, which measurements are possible?
Teachers' Resources
Why do this problem?
This problem encourages students to get into the real meaning of equations and graphical representation without getting bogged down in algebraic calculations or falling back into blind computation. It will help to reinforce the differences between different 'types' of equation.Possible approach
Key questions
- How can you tell if a certain point will match a certain equation type?
- How can you tell if a certain point will not match a certain equation type?
