Rain
How many dry days did Aisha have on her holiday?
Problem
On Aisha's holiday, $11$ days had some rain.
A morning rain was always followed by a clear afternoon.
An afternoon rain was always preceded by a clear morning.
A total of $9$ mornings and $12$ afternoons were clear.
How many days had no rain at all?
This problem is taken from the World Mathematics Championships
Student Solutions
Counting half-days
"A morning rain was always followed by a clear afternoon. An afternoon rain was always preceded by a clear morning," means that rain comes in half-days - there were no full days of rain.
So 11 days had some rain means, there were 11 half-days of rain.
"A total of nine mornings and twelve afternoons were clear", which makes a total of 9 + 12 = 21 clear half-days.
So altogether there were 11 + 21 = 32 half-days in Aisha's holiday, which is the same as 16 days.
11 of those 16 days had some rain, so the other 5 had no rain.
Using diagrams for the days
Each day can be split into morning and afternoon, and rain or clear. So each day can be represented by an image:




We know that "A morning rain was always followed by a clear afternoon", so

is impossible, but

is possible.
We know that "An afternoon rain was always preceded by a clear morning", so

is still impossible, but

is possible.
We are asked how many days had no rain at all - so how many

days there were.
It rained on 11 days, so altogether there were 11 of

and

.
The other days were

, and a group of

days contain the same number of clear mornings as clear afternoons. So there must be the same number of clear mornings and clear afternoons left after 11 of

and/or

.
Altogether, there were 9 clear mornings and 12 clear afternoons, which is 3 more clear afternoons. So they must have been paired with 3 rainy mornings, so there were 3 more

days than

days.
To make a total of 11, there must have been 4

days and 7

days - leaving 5 clear mornings and 5 clear afternoons - so 5

days with no rain.
Using a Venn diagram

The information can be shown on a Venn diagram, where the totals for the circles are shown in brackets, and the overlap is what we are asked for - the number of days with clear mornings and clear afternoons.
The region outside both circles represents days which did not have clear mornings or clear afternoons - so days with rainy mornings and rainy afternoons. We know there were not any days like that, because "A morning rain was always followed by a clear afternoon", or "An afternoon rain was always preceded by a clear morning."
We also know that "eleven days had some rain". These are the days with clear mornings but not clear afternoons, and vice versa. So the total number of days in the parts of the circles which don't overlap -
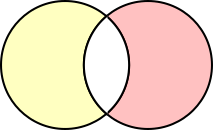
- must be 11.
Adding

to

counts the overlap ? twice, but

does not count the overlap ? at all. So

+

is the same as

+ 2 $\times$ ?.
So 9 + 12 = 21 is equal to 11 + 2 $\times$ ?.
So 2 $\times$ ? = 10, so ? = 5.

Be careful: here the Venn diagram needed to be set up correctly to be helpful. The Venn diagram on the right has the circles labelled for rain instead of clear.
It is useful to see that they don't overlap (since there were no days with rainy morning and rainy afternoon), and that the days we are counting are outside both circles. However, it is difficult to represent the rest of the information on this Venn diagram.
Using a two-way table
The information can be recorded in the table below.
| morning | ||||
|---|---|---|---|---|
| afternoon | rainy | clear | total | |
| rainy | ||||
| clear | ||||
| total | ||||
"A morning rain was always followed by a clear afternoon" and "An afternoon rain was always preceded by a clear morning" both tell us that there were $0$ days in the rainy, rainy box.
"A total of nine mornings and twelve afternoons were clear" allows us to fill in the totals $9$ and $12$.
To make calculations easier, two of the cells have been labelled $a$ and $b$. We know that $a+b=11$ because "eleven days had some rain".
| morning | ||||
|---|---|---|---|---|
| afternoon | rainy | clear | total | |
| rainy | $0$ | $b$ | $b$ | |
| clear | $a$ | $12$ | ||
| total | $a$ | $9$ | ||
From here, there are several possible approaches which are very similar. One is shown below.
We want to find the number of clear, clear days, which is $12-a$ or $9-b$.
So $12-a=9-b$.
Since $a+b=11$, $a=11-b$, so $12-a=12-(11-b)=1+b$.
Substituting this into $12-a=9-b$ gives $1+b=9-b$ so $2b=8$ and so $b=4$.
So $9-b=5$, and so there were $5$ days with no rain.
