Quadratic Rotation
The curve $y=x^2-6x+11$ is rotated through $180^\circ$ about the origin. What is the equation of the new curve?
Problem
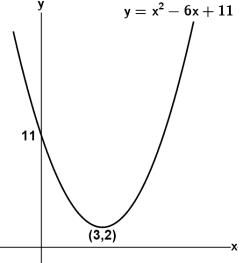
The curve $y=x^{2}-6x+11$ is rotated through $180^\circ$ about the origin.
What is the equation of the new curve?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
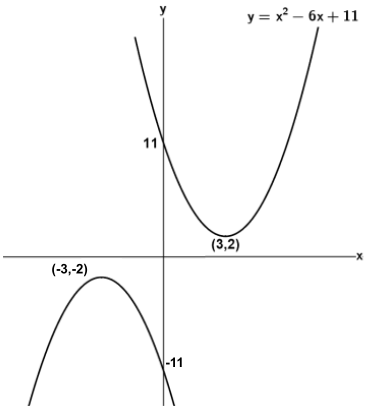
Answer: $y=-x^{2} - 6x - 11 $, which is the same as $y= -(x + 3)^{2} - 2$.
Completing the square
New graph is a negative quadratic with maximum $(-3,-2)$
The curve hasn't changed shape so $y=-x^2+...$ (not $y=-2x^2+...$ etc)
$\therefore$ equation is $y=-(x+3)^2-2$
Comparing coefficients
New graph has equation $y=ax^2+bx+c$
The curve hasn't changed shape but the quadratic is negative so $a=-1$
Intercept is $-11\Rightarrow c=-11$
$y=-x^2+bx-11$
And $(-3,-2)$ is on the graph so
$-2=-(-3)^2+b(-3)-11\\
\Rightarrow -2=-9-3b-11\\
\Rightarrow 18=-3b\\
\Rightarrow b=-6$
So the equation is $y=-x^2-6x-11$
Using $-x$ and $-y$
Rotation of $180^\circ$ about $(0,0)$ is the same as swapping $x$ for $-x$ and $y$ for $-y$
Swap $x$ for $-x$ and $y$ for $-y$ in the equation $y=x^2-6x+11:$
$$\begin{align} -y&=(-x)^2-6(-x)+11\\
\Rightarrow -y&=x^2+6x+11\\
\Rightarrow y&=-x^2-6x-11\end{align}$$
