Proof of Pick's theorem
Follow the hints and prove Pick's Theorem.
Problem
Pick's Theorem states that if a polygon has vertices with integer coordinates (lattice points) then the area of the polygon is $i + {1\over 2}p - 1$ where $i$ is the number of lattice points inside the polygon and $p$ is the number of lattice points on the perimeter of the polygon.
Define Pick's function for a polygon $P$ as $$F(P)= {\rm area }(P) - \left(i + {1\over 2}p - 1\right)$$ where $i$ and $p$ are defined as above. To prove Pick's Theorem, we have to show that this function takes the value zero for all planar polygons. You will need to use the fact that any polygon can be split into a finite number of non-overlapping triangles.
| The sequence of five steps in this proof starts with 'adding' polygons by glueing two polygons along an edge and showing that if the theorem is true for two polygons then it is true for their 'sum' and 'difference'. | Image
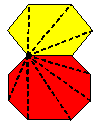
|
| The next step is to prove the theorem for a rectangle, then for the triangles formed when a rectangle is cut in half by a diagonal, then for the general triangle (labelled $T$ in the diagram below), and finally for any planar polygon because it can be built up from 'adding' triangles. Although the proof is long it is simply a matter of counting points. | Image
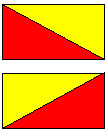
|
(1) Let $P_1$ and $P_2$ be non-overlapping polygons that abut along a common edge $AB$. Let $P$ be the union of $P_1$ and $P_2$ and $i, i_1$ and $i_2$ the lattice points inside and $p, p_1$ and $p_2$ the lattice points on the perimeter of $P, P_1$ and $P_2$ respectively. Prove that if Pick's function is zero for any two of these polygons it must be zero for the third.
(2) Prove that Pick's function is zero for the rectangle with vertices $(0,0), (a,0), (0,b)$ and $(a,b)$ where $a$ and $b$ are integers.
(3) Two triangles are produced when the rectangle with vertices $(0,0), (a,0), (0,b)$ and $(a,b)$ is cut in half by one or other of the diagonals. Prove that Pick's function is zero for these triangles and hence that Pick's Theorem holds for any right-angled triangle with sides parallel to the axes.
(4) Prove that Pick's Theorem holds for the general triangle $T$ shown in this diagram. (5) Prove that Pick's Theorem holds for any planar polygon.
Image
|
Getting Started
Follow the five steps in the question. These steps lead you to the required proof.
(1) Here you are glueing 2 polygons along a common edge and the area of the 'sum' of the polygons is the sum of the areas of the individual polygons. Decide which lattice points on the common edges become interior lattice points to the new polygon and which are on the edge of the new polygon and make sure none of these is counted twice.
(2) Proving Pick's Theorem for a rectangle simply involves counting lattice points.
(3) Now deduce Pick's Theorem for right-angled triangles.
(4) Now you know Pick's Theorem holds for rectangles and right-angled triangles deduce that it holds for the general triangle.
(5) Finally deduce Pick's Theorem for the general plane polygon using the earlier parts of the proof.
Student Solutions
Here is another excellent solution from Andrei of Tudor Vianu National College, Bucharest, Romania.
I shall prove Pick's Theorem by proving that Pick's function $$F(P)= {\rm area }(P) - (i + {p\over 2} - 1)$$ is 0 for any planar polygon, following the steps from the problem.
(1) Let $P_1$ and $P_2$ be two polygons with a common edge, $P$ the union of $P_1$ and $P_2$, $i$, $i_1$, $i_2$ the lattice points inside the 3 polygons, and $p$, $p_1$, $p_2$ the lattice points on the perimeters of the 3 polygons.
Let $x$ be the number of lattice points of the common edge of $P_1$ and $P_2$. It is clear that area($P$) = area($P_1$) + area($P_2$)
Image
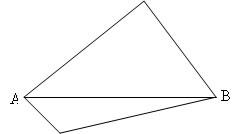
| From the figure I observe that: $i = i_1 + i_2 + x - 2$ $p = p_1 + p_2 - 2x + 2.$
Now, I shall calculate $F(P)$: |
\begin{eqnarray} F(P)&=& {\rm area }(P) - (i + {p\over 2} - 1)\\ &=& {\rm area }(P_1)+{\rm area }(P_2)-i_1 -i_2 -x + 2 - {p_1 \over 2} - {p_2\over 2} + x - 1 + 1 \\ &=& {\rm area }(P_1)+{\rm area }(P_2)-i_1 -i_2 - {p_1\over 2} - {p_2\over 2} + 2\\ &=& {\rm area }(P_1) - (i + {p_1\over 2} - 1)+{\rm area }(P_2)- (i + {p_2\over 2} - 1)\\ &=& F(P_1) + F(P_2) \end{eqnarray} So, if Pick's function is zero for any two of these polygons it must be zero for the third. This means that if Pick's Theorem holds for any two of these polygons it must hold for the third. As a generalization, $$F(P_1+P_2+ ... +P_n) = F(P_1) + F(P_2) + ... +F(P_n).$$ So, $F$ is additive.
(2) Now I shall prove Pick's Theorem for a rectangle with vertices $(0,0), (a,0), (a,b), (0,b)$.
${\rm Area}(P) = ab$, $i = (a - 1)(b - 1)$ and $p = 2(a + b).$ So $$F(P) = ab - (a-1)(b-1) - (a+b) + 1 = 0.$$ Any rectangle with sides parallel to Ox and Oy could be translated to a rectangle of the given form.
(3) If the rectangle is split into two triangles by a diameter then each triangle has the same area and the same number of interior points and the same number of points on the perimeter and hence Pick's function must take the same value for each triangle. By parts (1) and (2) Pick's function must be zero for such triangles.
When a polygon with vertices at lattice points is translated so that the image has vertices at lattice points there is no change in area, or in the number of interior lattice points, or in the number of lattice points on the perimeter. Hence Pick's function is zero for all rectangles and for any right-angled triangle which has twosides parallel to the coordinate axes.
Image
| (4) Now I shall prove the theorem for any triangle.
Let $T$ be a triangle. Any shape of triangle can be enclosed in a rectangle with edges parallel to the coordinate axes, as in the diagram, by adding at most three triangles.
From part (1): $$ F(T+T1+T2+T3) = F(T) + F(T1) + F(T2) + F(T3). $$ But from part (2): $$ F(T+T1+T2+T3) = 0 $$ and from part (3): $$ F(T1) = F(T2) = F(T3) = 0. $$ From these relations, I observe that $F(T) = 0$. |
(5) As any polygon can be split into triangles and rectangles, the theorem is proved.
Teachers' Resources
Image

| We are allowed to assume that any polygon, convex or not, can be split into a finite number of non-overlapping triangles.
However in this proof we assume that the interior of the polygon does not have any holes like the red polygon shown with a yellow hole in the diagram. Pick's formula is related to Euler's formula and ${\rm area }(P) = i + {1\over 2}p - q$ where $q$ depends on the number of holes. |
