Population dynamics - part 4

Fourth in our series of problems on population dynamics for advanced students.
Age
16 to 18
Challenge level
filled star filled star empty star
Exploring and noticing Working systematically Conjecturing and generalising Visualising and representing Reasoning, convincing and proving
Being curious Being resourceful Being resilient Being collaborative

Problem



The Logistic Map

The logistic map is the discrete case of the logistic equation, given by:   $\frac {\mathrm{d}y}{\mathrm{d}t}=ry(1-\frac{y}{Y})$

We then approximate to deduce the discrete case:$$ \begin{align*}  \frac{y_{n+1}-y_n}{\Delta t} &\approx ry_n\left(1-\frac{y_n}{Y}\right) \\ y_{n+1} &\approx r \Delta t y_n \left(1-\frac{y_n}{Y}\right)+y_n \\ y_{n+1}&=(1+r \Delta t)y_n-\frac {r\Delta t}{Y}{(y_n)}^2 \\ y_{n+1}&=(1+r \Delta t)y_n\Bigg( 1-\bigg(\frac{r\Delta t}{1+r\Delta t}\bigg)\frac{y_n}{Y}\Bigg) \end{align*} $$

Let $\lambda=1+r\Delta t$ and $x_n=\frac {r\Delta t}{1+r \Delta t} \frac {y_n}{Y}$ . Then our equation becomes: $$x_{n+1}=\lambda x_n (1-x_n) $$ This is the logistic map. We can also think of it as a function $x_{n+1}=f(x_n)$.

 

Finding Equilibrium Points

Question:   A fixed point implies $x_{n+1}=x_n$ . Find the fixed points by solving $$ \lambda x_n (1-x_n) = x_n $$ To determine the stability of these points, we are going to find the stability, by investigating the function for values nearby the equilibrium points.

 

Start by supposing that $x_n=X$ is a fixed point. This means that $f(X)=X$. 

To find a value near the equilibrium point, let $x_n=X+\epsilon{_n}$ where $\epsilon_n < < 1$. Then using the Taylor expansion: $$ \begin{align*} x_{n+1}&=f(x_n) \\ X+\epsilon_{n+1} &= f(X+\epsilon_n) \\ &=f(X)+\epsilon_n f'(X)+... \end{align*}$$

We neglect the higher-order terms to get: $$X+\epsilon_{n+1}=f(X)+\epsilon_n f'(X)$$ Now from above we saw that $f(X)=X$ , so we can simplify to get: $$\epsilon_{n+1} \approx f'(X) \epsilon_n$$ A fixed point, X, is then stable if:   $\Bigg|\frac{\epsilon_{n+1}}{\epsilon_n}\Bigg | =\Bigg |f'(X)\Bigg | < 1$

 

Question:  Given that $f'(x)=\lambda-2\lambda x$ , find the stability of the fixed points $x_n=0$  and  $x_n=1-\frac{1}{\lambda}$

 

Different Cases of Stability

Below are some graphs of the logistic map for different values of $\lambda$ .

 

         Case 1: $\lambda< 1$

Only fixed point is 0, which is stable:

Population Dynamics - part 4

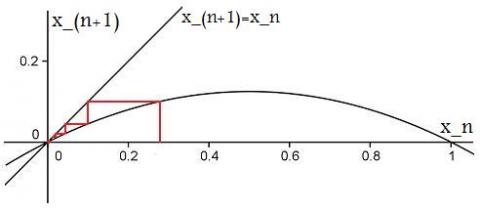
         Case 2: $1< \lambda < 2$

Unstable fixed point at 0 and stable fixed point at $1-\frac{1}{\lambda}$

Population Dynamics - part 4

 

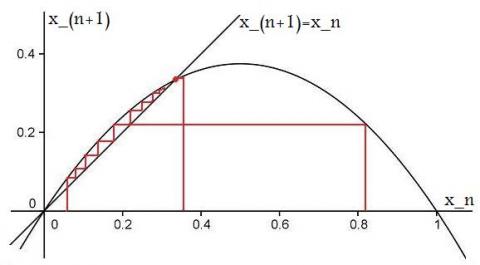
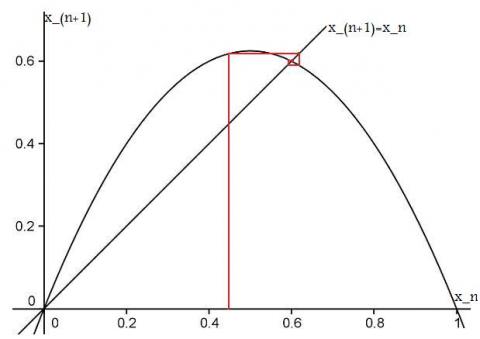
Question:  Can you find the stability for the case $2< \lambda < 3$  ? 

 

Below is a picture of some fantastic fractal behaviour which occurs for $3< \lambda< 4$.

Population Dynamics - part 4

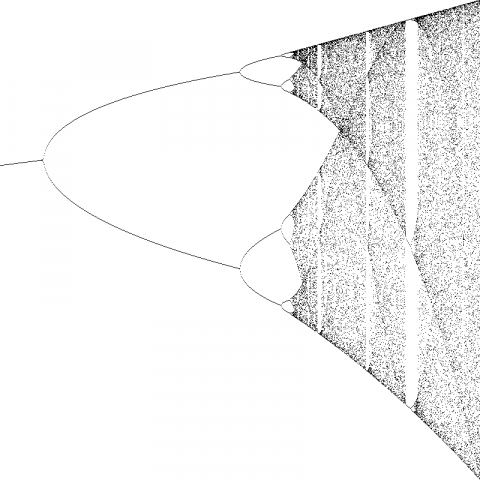
Question:  Can you relate these values of $\lambda$ to what would actually be occuring in a population of organisms?