Polar bearings
Problem
Often when we want to indicate the position of an object, we refer to its distance and direction. We can use a coordinate system based on this, giving the distance from an origin and a direction as an angle measured anticlockwise from the horizontal.
Here is a map of Scotland.
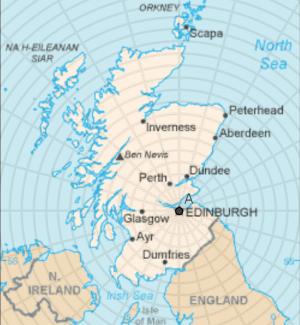
The grid on this map measures from an origin at Edinburgh, and the lines indicate distances from Edinburgh at 20km intervals.
Lines are marked radiating from Edinburgh at $15^\circ$ or $\frac{\pi}{12}$ radian intervals.

Dundee is to the north and slightly to the east of Edinburgh. I need to travel a distance of approximately 60km in a direction $\frac{5\pi}{12}$ anticlockwise from the horizontal.
I can express the position of Dundee in polar coordinates as $(60, \frac{5\pi}{12})$.
The distance coordinate is usually called $r$, and the direction is $\theta$, so a polar coordinate pair is $(r, \theta)$.
Can you express the position of some other places on the map using polar coordinates?
By giving a functional relationship between $r$ and $\theta$, we can represent curves on the polar coordinate plane. Can you sketch the following functions?
a) $r=2$
b) $\theta = \frac{\pi}{4}$
c) $r=\theta$
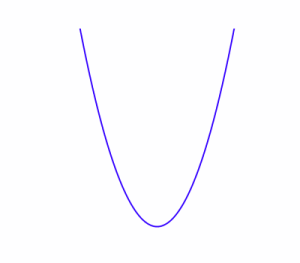
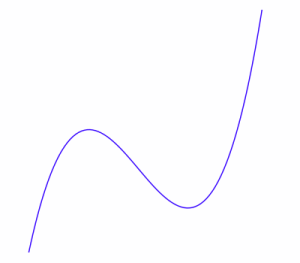
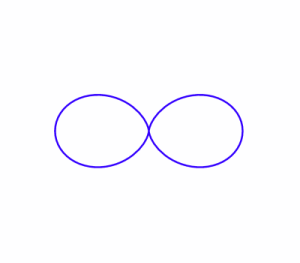
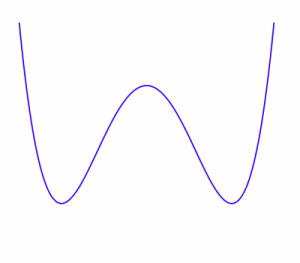
Here are some sketches of curves. You can choose where to put the origin.
Which ones do you think it would be easier to express in Cartesian $(x,y)$ coordinates?
Which ones do you think would be easier to express in Polar $(r, \theta)$ coordinates?
|
A |
B |
|
C |
D |
|
E |
Image

F |
|
G |
H |
Image

I |
Image

J |
Are there any graphs where you could easily use either coordinate system?
If the origin had been specified, how might it have affected your decision?
Try to find functional forms, in either cartesian or polar coordinates, to create graphs that closely resemble those above.
You may wish to use graph plotting software to help you; some useful graphing tools can be found here.
You can read more about Polar Coordinates in this article.
Earth Orbit is a challenging problem about orbits that shows the real-life applications of polar coordinates.
Getting Started
The article Where? Over There... introduces polar coordinates, so it might be useful to read it through to help you to get started on this problem.
Teachers' Resources
Why do this problem?
When students meet polar coordinates for the first time, they are sometimes reluctant to engage with a new representation when they can already do so much with the powerful cartesian representation to which they are accustomed. This problem defines polar coordinates through the familiar idea of specifying a location using a bearing and a distance, and then offers students the opportunity to reflect on occasions when the polar representation might be better suited than the cartesian.
Possible approach
Share with students the map of Scotland from the problem (available on a PowerPoint or as a worksheet).
"The grid on this map measures from an origin at Edinburgh, and the lines indicate distances from Edinburgh at 20km intervals. Lines are marked radiating from Edinburgh at $15^\circ$ or $\frac{\pi}{12}$ radian intervals. Imagine you were in Edinburgh. How might you describe the position of Dundee?"
Students' answers should provoke a need to standardise the way the distance and direction are expressed.
"Mathematicians often use a representation called polar coordinates when they want to specify a position based on its distance and direction from the origin. We measure the angle from the horizontal, usually in radians, and the distance, and we write $(r, \theta)$ for the coordinate pair. If Dundee's polar coordinate position is $(60, \frac{5\pi}{12})$, can you write down the positions of some other places from the map?"
Give students a few minutes to have a go, and then share answers.
"As with $x$ and $y$ in cartesian coordinates, we can write an equation linking $r$ and $\theta$ to plot graphs. In cartesian coordinates, $y=$ constant, $x=$constant and $y=x$ form straight lines horizontally, vertically and at $45^{\circ}$. Talk to your partner and see if you can sketch the polar coordinate graphs $r=$ constant, $\theta =$ constant and $r=\theta$."
While students work on this, circulate to check that they have understood the definitions. If they are stuck, you could ask questions like:
"Choose an origin. Can you plot some points where $r=1$?
"Can you plot some points where $\theta=\frac{\pi}{4}$?
"Can you plot some points where $r = \theta$?"
Next, introduce the main part of the problem:
"Here are ten different curves. With your partner, decide whether you'd rather draw it using cartesian or polar coordinates. You can choose where the origin goes. Once you've decided, see if you can work out a functional form that results in graphs like the ones you've been given."
This works particularly well if students have access to a graphing package or graphical calculator that can operate in cartesian and polar mode. Some useful graphing tools are suggested here. Students can then try out their ideas to recreate the polar graphs.
Finally, bring students together to discuss what they have found out. This PowerPoint has all ten images if you want to display them one at a time for discussion. Invite students to say where they would choose to place the origin, and what sort of functional form they think the graphs have. This could be checked using graphing software.
Possible extension
Earth Orbit offers a very challenging extension for students who are interested in applications of polar coordinates to solve real-world problems.
Possible support
The article Where? Over There... provides a gentle introduction to polar co-ordinates that students could read through and work on before tackling the main part of this problem.