Plates of Biscuits
Problem
There are $12$ plates of biscuits with $3$ identical biscuits on each plate.
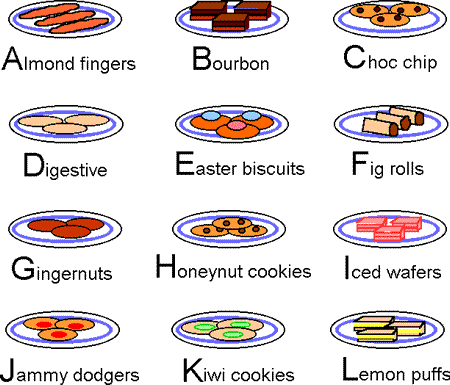
(They are named simply to help identify them by a letter!)
Can you rearrange the biscuits on the plates so that
- The $3$ biscuits on each plate are all different
and - There is no plate with two biscuits the same as two biscuits on another plate?
For example, if you have one plate of 'A, D and F' then you cannot have another with both 'A and D' or 'A and F' or 'D and F'.
Getting Started
Student Solutions
One way of making sure all possibilities were included came from Ms Brown's class, at Alice Smith International School, in Kuala Lumpur, Malaysia, at the end of these solutions. It was a very clearly set out table created using a spreadsheet.
Emma and Abi of Moorfield Junior School found the following combinations of three biscuits from the $12$ different varieties, this was the same as that sent in by Sarah and Helen from Glenmead Primary in Birmingham. They show their answers as a list, but first they explain the strategy they used to help them with so many possibilities:
First, we started with alphabetically, ABC, DEF, GHI and
JKL.
Then we did the first letter of the first three biscuits
(ADJ).
Next we took the second letters (BEH) of each plate of
biscuits.
Finally, we sorted out the ones left over.
The possible plates of biscuit varieties that the girls came up with were:
| HIG | HKJ | ABC | DEF |
| ADJ | EBH | AIK | FIC |
| KLA | DBG | LEC | FLG |
Prateeksha , from Riccarton Primary School, shows a slightly different strategy. It is a list like Emma and Abi's but can you see how the information has been organised in this list? The organisation is what shows Prateeksha's thinking.
| Plate A contains biscuits A, H, L |
| Plate B contains biscuits B, H, K |
| Plate C contains biscuits C, B, A |
| Plate D contains biscuits D, A, J |
| Plate E contains biscuits E, B, D |
| Plate F contains biscuits F, E, C |
| Plate G contains biscuits G, J, K |
| Plate H contains biscuits H, G, E |
| Plate I contains biscuits I, D, C |
| Plate J contains biscuits J, L, I |
| Plate K contains biscuits K, I, F |
| Plate L contains biscuits L, G, F |
Is this list the same as Terry and Daren's from Alma Primary School in London?
| plate 1. AKL |
| plate 2. BDK |
| plate 3. FIJ |
| plate 4. DGI |
| plate 5. BEH |
| plate 6. FGL |
| plate 7. BGJ |
| plate 8. AHI |
| plate 9. CEJ |
| plate 10. ACF |
| plate 11. CHK |
| plate 12. DEL |
Helen and Joanna from W.C.P.School in Manchester sent in a list of their 'plates' and used letters to represent the biscuit varieties, as did James from Girton Glebe Primary School near Cambridge. Although the order of their answers was different, the combinations were the same.
Hannah, Amy, Jenny
and Emma , also from
Moorfields School, seem to have a completely different way of
figuring out their solution. But have they?
Can you see what they have done?
- Almond fingers on plates 1,2,3
- Bourbon on plates 4, 5, 9
- Chocolate chip on plates 7, 8, 9
- Digestive on plates 5, 6,10
- Easter biscuits on plates 4, 8,12
- Fig rolls on plates 2, 4, 7
- Ginger-nuts on plates 3, 9, 11
- Honey cookies on plates 2,10,11
- Iced Wafers on plates 1, 5, 8
- Jammy Dodgers on plates 3, 6, 10
- Kiwi cookies on plates 1, 7,6
- Lemon puffs on plates 6,11,12
But how do you keep track of all that information? This is what Alex from Brecknock School did:
I started with abc, then def, ghi, jkl and then mixed them
up.
I made a list of all the biscuits as they were used, after that I
crossed out a letter every time I used one of that type.
| a | d | g | j | l | c | l | f | b | j | k | b |
| b | e | h | k | h | e | h | i | k | c | a | f |
| c | f | i | l | d | g | a | j | i | d | e | g |
Hmm, it looks like 'a and f' in the centre line are not matched with other biscuits. Why do you think that is?
Oskar , a fellow pupil from Brecknock Primary, started with A(lmond finger) and I moved 1 A forward 1 place and another A forward 2 places. I did the same with the next plate then the next plate and so on. The solution ended up like this:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| k | l | a | b | c | d | e | f | g | h | i | j |
| l | a | b | c | d | e | f | g | h | i | j | k |
| a | b | d | e | f | g | h | i | j | k | l |
Nathan , also from
Brecknock explains; first I wrote a table .
I started with kbc then I made sure that I used each biscuit
once
I continued with the rest of the biscuits. When I had used all the
biscuits I had to mix the biscuits about. This was my answer:
kbc, def, ahf, jk, dbe, bgc, jhb, fki, aij, iel, lgd, gca.
The students of Ms Brown's class also organized their information in a table , but in different way then Oskar. Did they arrive at a different answer the other pupils above?
They begin by explaining their notation. They used a combination of letters (for the variety of biscuit) and numbers (to show if it was the first, second or third biscuit selected).
Notation:
A lmond Fingers = A1 (biscuit 1), A2 (biscuit 2),
A3 (Biscuit 3).
B ourbon = B1, B2, B3.
C hocolate Chip = C1, C2, C3.
D igestive = D1, D2, D3.
E aster Biscuits = E1, E2, E3.
F ig Rolls = F1, F2, F3.
G ingernuts = G1, G2, G3.
H oneynut cookies = H1, H2, H3.
I ced Wafers = I1, I2, I3.
J ammy Dodgers = J1, J2, J3.
K iwi Cookies = K1, K2, K3.
L emon puffs = L1, L2, L3.
Working it out:
Altogether there are $36$ Biscuits.
$12$ types of biscuits and $12$ plates.
So, what did they do with the information? They used a spreadsheet and built a table like this. One of the pupils explains:
Put A-B-C together, D-E-F together, G-H-I together and J-K-L together:
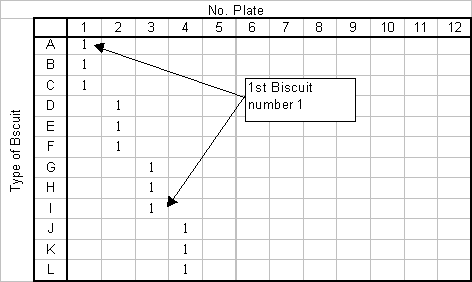
Now there are $2$ of each biscuit left.
