Pile driver
Weekly Problem 38 - 2015
Where does the line through P that halves the figure shown meet the edge XY?
Where does the line through P that halves the figure shown meet the edge XY?
Age
11 to 14
Challenge level
Problem
Image
The diagram shows a figure made from six equal, touching squares arranged with a vertical line of symmetry. A straight line is drawn through the bottom corner $P$ in such a way that that the area of the figure is halved.
Where will the cut cross the edge $XY$?
If you liked this problem, here is an NRICH task that challenges you to use similar mathematical ideas.
Student Solutions
The small square on top will be in the upper half of the divided figure. Now consider the figure formed by moving this square to become an extra square on the left of the second row, as shown.
Image
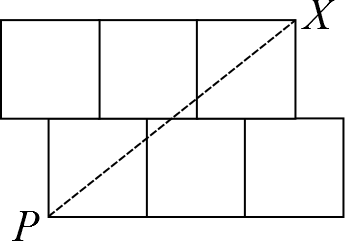
It may now be seen from the rotational symmetry of the figure that the line $PX$ splits the new figure in half- with that small square in the upper half.
Therefore the line which halves the area of the original figure cuts the edge $XY$ at $X$.
Therefore the line which halves the area of the original figure cuts the edge $XY$ at $X$.