PDF stories
Invent scenarios which would give rise to these probability density functions.
Problem
Consider the following curves, with scales chosen so as to make their integrals between the endpoints equal to 1. Curves with a finite domain are indicated with a vertical line, and the axes are assumed to intersect at the origin. Make up some statistical situations, either from mathematics or from science, which would plausibly result in one of these curves as a probability density function.
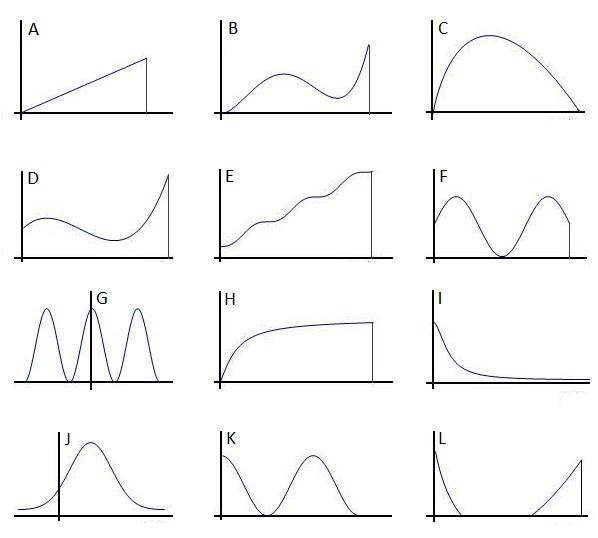
Keep your eyes open for curves in other areas of mathematics.Would they be potential candidates (ignoring scale) for probability density functions? What mathematical descriptions might accompany them? What scientific situations might they describe?
Pure maths extension: Find algebraic expressions for curves such as these, with parameters and domain chosen so as to make their integrals equal to 1 (exactly or approximately, as approriate)
Teachers' Resources
Why do this problem?
This problem is a good vehicle for fostering thinking about probability density functions and getting some talk into the statistics classroom. It could be used alongside a traditional introduction to the concepts to probability density functions or as a discussion-based consolidation. It can be approached from various levels of sophistication: all students should be able meaningfully to engage with it, and you can come back to the ideas at several points during a course of statistics.
Possible approach
Key questions
Possible extension
Possible support
