Partly painted cube poster
Problem
The poster is available as a PDF, or the image below can be clicked on to enlarge it.
Student Solutions
Answer: It was a 5 by 5 by 5 cube with four faces painted and two opposite faces unpainted
Working backwards from the result
45 = 3$\times$3$\times$5
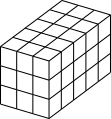
It must have been a 5 by 5 by 5 cube because the longest side is 5 cubes long. We can't add any more painted cubes to that side.

Need to add a face to each side of the 3 by 3 face $\therefore$ we will add 4 faces like this
Painting cube faces
43 = 64 $\gt$ 45
53 = 125 $\gt$ 45
63 - even if you painted all of the faces, there would be 43 = 64 unpainted cubes in the middle. So it must be 43 or 53
64, each face 16. Paint one face, 48 cubes unpainted. There is no way to paint just 3 cubes.
125, each face 25. Paint one face, 100 left unpainted, 5 by 5 by 4 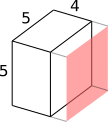
Painting the opposite face would leave 75 unpainted (remove a 5 by 5 face)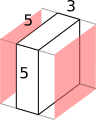
Painting any other face would leave 80 left unpainted (remove a 5 by 4 face) 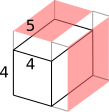
Paint opposite face: 5 by 5 by 3. You can't paint 25 again because no side can be shorter than 3. Paint 15 cubes to leave 60 unpainted, 5 by 4 by 3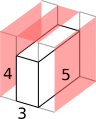
Then painting the bottom face will remove another 15 cubes, leaving 45 unpainted.

