Partly Painted Cube
Problem
Partly Painted Cube printable sheet
Jo made a cube from some smaller cubes. She painted some of the faces of the large cube, and then took it apart again.
She counted her cubes and noticed that 45 cubes had no paint on them at all.
Dan made a cube the same size as Jo's large cube, and also painted some of the faces.
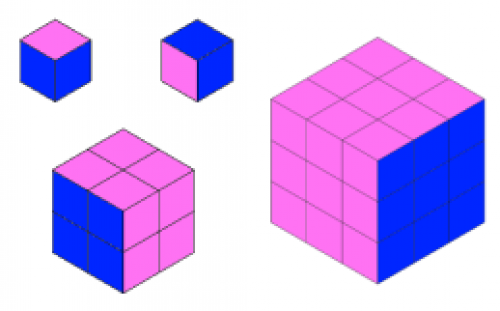
Now explore the number of unpainted cubes for some other sizes of cube. Here are some questions you might like to consider:
- If the number of small cubes along each edge is $n$, can you find expressions for the number of unpainted cubes when you paint 1, 2, 3, 4... faces?
- The number of unpainted cubes can always be expressed as the product of three factors. What can you say about these factors?
- There is only one way to end up with 45 unpainted cubes. Are there any numbers of cubes you could end up with in more than one way?
- How can you convince yourself that it is impossible to end up with 50 unpainted cubes?
Click here for a poster of this problem
Getting Started
How many different ways could you paint two faces of a cube? Or three? Or four?
Can you work out a way of counting how many cubes are left unpainted in each case?
Student Solutions
Well done to Rajeev from Fair Field Junior School who sent us this solution:
Jo noticed that when she painted some of the faces of her cube then $45$ faces had no paint on them. Her cube was $5 \times 5 \times 5$, and $4$ faces were painted, so $80$ cubes had paint on them and $45$ cubes were unpainted.
Here is a table showing the number of painted cubes for different sizes of cube and numbers of faces painted:
|
Dimensions of
Cube
|
Number of
Cubes
|
1 face
painted
|
2 opposite
faces painted
|
3 faces
painted
|
4 faces
painted
|
5 faces
painted
|
6 faces
painted
|
| $2\times2\times2$ | $8$ | $4$ | $8$ | $8$ | $8$ | $8$ | $8$ |
| $3\times3\times3$ | $27$ | $9$ | $18$ | $21$ | $24$ | $25$ | $26$ |
|
$4\times4\times4$
|
$64$ | $16$ | $32$ | $40$ | $48$ | $52$ | $56$ |
| $5\times5\times5$ | $125$ | $25$ | $50$ | $65$ | $80$ | $89$ | $98$ |
| $6\times6\times6$ | $216$ | $36$ | $72$ | $96$ | $120$ | $136$ | $152$ |
| $17\times17\times17$ | $4913$ | $289$ | $578$ | $833$ | $1088$ | $1313$ | $1538$ |
| $n \times n \times n$ | $n^3$ | $n^2$ | $2n^2$ | $3n^2-2n$ | $4n^2-4n$ | $5n^2-8n+4$ | $6n^2-12n+8$ |
When Jo had to paint the 2nd face she painted the opposite face. I noticed that it does make a difference in what pattern the faces are painted. The above table applies when painting the second face the one opposite the painted face is painted and after that then you can paint the other faces in any order. Another way to do it is to paint the adjacent face- so after painting the 1st face(say right side) you paint the 2nd face adjacent to it and the 3rd face (say top face)painted must be touching the two painted faces and the 4th face (say bottom face) and the 5th face any remaining side.
Rajeev highlights the idea that painting faces in a different arrangment affects the number of painted cubes. Here is a table with all possible arrangements.
When faces of a larger cube are painted then the number of unpainted cubes depends upon whether the opposite or the adjacent face was painted when painting the second face. Jo's 2nd face was the opposite face so when she painted the 4th face she had $45$ unpainted cubes. If Jo had started painting the adjacent face then she would have been left with $48$ cubes in a $5\times5\times5$ cube.
There is more than one way to end up with any number of cubes - you can end up with $27$ unpainted faces when you paint three adjacent faces in a $4\times4\times4$ cube and also in a $5\times5\times5$ cube when you paint all $6$ faces.
Another way to think about this problem is to imagine removing all the painted cubes and leaving behind a cuboid each time. What can you say about the difference between the largest and smallest dimension of such a cuboid?
Elizabeth, a teacher at Rutherford College, New Zealand, has sent us this very nice diagram that demonstrates visually what happens when you remove a number of faces from an $n \times n \times n$ cube.
Write $N$ for the number of unpainted cubes remaining.
The first thing to notice is that when we remove the painted faces, we will always be left with an unpainted cuboid.
When one face i
When the two adjacent faces are painted, we are left with a $n \times (n-1) \times (n-1)$ unpainted cuboid. The diagram to the right shows what happens when the front-left and front-right faces are painted.
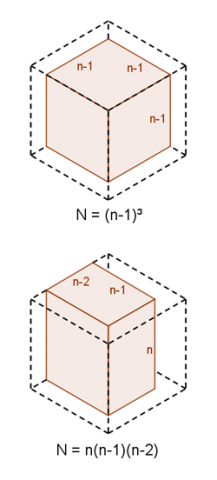
If the painted faces meet at a vertex, we are left with an $(n-1) \times (n-1) \times (n-1)$ unpainted cube. The diagram to the right shows what happens when we remove the front-left, front-right and top faces.
If there are two opposite faces painted (and one other), then we are left with an $n \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when we remove the front-left, front-right and back-right faces.
When there are four faces painted, there are two possible configuations again. The unpainted faces must either be adjacent or opposite.
If the unpainted faces are adjacent, then we are left with an $ (n-1) \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when the front-left, front-right, back-right and top faces are removed.
If the unpainted faces are opposite, so that the painted faces form a ring shape, then we are left with an $n \times (n-2) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when the front-left, front-right, back-left and back-right faces are removed.
If five faces are removed, there is only one possible configuration, in which we are left with an $ (n-1) \times (n-1) \times (n-2)$ unpainted cuboid. The diagram to the right shows what happens when only the bottom face is unpainted.
When all six faces are painted, so all are removed, what remains is a cube of side-length $n-2$, as shown in the diagram to the right.
This demonstrates that the number of unpainted cubes can always be written as the product of three factors which differ from each other by no more than $2$.
We can use this to see how we can leave $45$ cubes unpainted. Since $45 = 5 \times 3 \times 3$, we can write this as $45 = 5 \times \left( 5-2 \right) \times \left( 5-2 \right)$. This means we can start with a $5 \times 5 \times 5$ cube, and then paint two pairs of opposite faces to leave $45$ unpainted cubes.
This also explains why we cannot leave exactly $50$ cubes unpainted. For this to be possible, we would have to find three numbers that multiplied to give $50$ but differed by no more than $2$. This is impossible:
$50 = 2 \times 5^2$, as a product of prime factors.
We can write $50$ as the product of three positive integers as $2 \times 5 \times 5$, or if one of the integers is $1$, one of the others will have to be at least $5$.
Both of these cases have differences of more than $2$, so we cannot leave $50$ unpainted cubes.
Teachers' Resources
Why do this problem?
There are many ways of tackling this problem, so there is an opportunity for students to share insights and consider the benefits of the different approaches.
Students have an opportunity to play with algebra they might not normally meet, forming cubic expressions that can be related back to the physical properties of the cuboids they represent.
This problem allows students to model the way mathematicians work, by taking a starting point and then asking their own questions and making conjectures that may lead to generalisations.
This problem lends itself to collaborative working, both for students who are inexperienced at working in a group and students who are used to working in this way.
Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.
Possible approach
This printable worksheet may be useful: Partially Painted Cube.
This is an ideal problem for students to tackle in groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on this task should be measured by how effectively the members of the group work together as well as by the solutions they reach.
Hand out this task sheet ( Word, pdf) to each group and make it clear that everyone needs to be ready to share their findings with the rest of the class at the end.
You may want to make isometric paper, cubes, poster paper, and coloured pens available for the Resource Manager in each group to collect.
When groups have had a chance to work on the first two questions (this may take more than a lesson!) allow some whole-class time for groups to share their thoughts, questions, and ideas for possible lines of enquiry. There are some suggestions of possible questions to consider in the problem which can be used as prompts for classes who are struggling to come up with conjectures of their
own.
While groups are working, label each table with a number or letter on a post-it note, and divide the board up with the groups as headings. Listen in on what groups are saying, and use the board to jot down comments and feedback to the students about the way they are working together.
You may choose to focus on the way the students are co-operating:
Group A - Good to see you sharing different ways of thinking about the problem.
Group B - I like the way you are keeping a record of people's ideas and results.
Group C - Resource manager - is there anything your team needs?
Alternatively, your focus for feedback might be mathematical:
Group A - I like the way you are considering the structure of the cube.
Group B - You've identified the different combinations of faces that can be painted - what could you do with this information?
Group C - Good to see that someone's checking that the answers are in line with your predictions.
Make sure that while groups are working they are reminded of the need to be ready to present their findings at the end, and that all are aware of how long they have left.
We assume that each group will record their diagrams, reasoning and generalisations on a large flipchart sheet in preparation for reporting back. There are many ways that groups can report back. Here are just a few suggestions:
- Every group is given a couple of minutes to report back to the whole class. Students can seek clarification and ask questions. After each presentation, students are invited to offer positive feedback. Finally, students can suggest how the group could have improved their work on the task.
- Everyone's posters are put on display at the front of the room, but only a couple of groups are selected to report back to the whole class. Feedback and suggestions can be given in the same way as above. Additionally, students from the groups which don't present can be invited to share at the end anything they did differently.
- Two people from each group move to join an adjacent group. The two "hosts" explain their findings to the two "visitors". The "visitors" act as critical friends, requiring clear mathematical explanations and justifications. The "visitors" then comment on anything they did differently in their own group.
Key questions
If your focus is effective group work, this list of skills may be helpful (Word, pdf). Ask learners to identify which skills they demonstrated, and which skills they need to develop further.
If your focus is mathematical, these prompts might be useful:
What solid are you left with when you remove the painted cubes? How can you express this algebraically (for 1, 2, 3... faces painted)?
Possible support
By working in groups with clearly assigned roles we are encouraging students to take responsibility for ensuring that everyone understands before the group moves on.
Painted Cube provides a suitable introduction to some of the ideas met in this problem.
Possible extension
Devise a method for determining whether any given number of unpainted cubes can arise from painting whole faces of a large cube, and if so, how it can be done.