Painting by functions
Use functions to create minimalist versions of works of art.
Problem
In minimalist, abstract or computer generated art a real object is often represented by a simplified set of shapes and curves.
For example, this image of the famous artist Mondrian might be transformed or represented by transformations of standard mathematical functions as follows:
Image
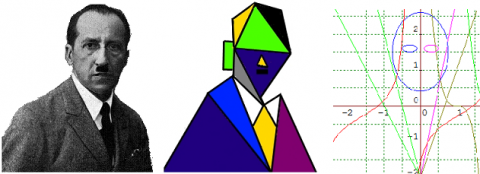
Consider some objects and works of art. Think how they might be broken down into shapes or segments of lines and curves. How many such shapes or line and curve segments would be needed to give a recognisable abstract impression of the pictures? Imagine how you could encode your lines and curves mathematically by imposing a coordinate grid on the picture.
Use a graphing software package to create your impressions mathematically. Your toolkit contains the standard mathematical functions: Polynomials, sin, cosh, sinh and also the techniques of composition and transformation of functions.
You might want to print off the picture, highlight the segments of the curves of interest and colour according to the colouring schemes in Painting by Numbers.
Please send us any of your creations!
If you want to focus on pictures made with straight lines, see the problem Painting Between The Lines.
NOTES AND BACKGROUND
The mathematical issues raised in this problem are directly related to the creation of computer generated art where images are typically encoded mathematically; indeed if you zoom in closely to any digital image you will see that it is encoded as squares or blocks of uniform colours which give the impression of an analogue image.
In computer gaming, images are first represented minimally and digitally using mathematics; the next phase is to animate the images.
You can read more about the mathematics of art on the Plus website pages
Digital Art by Lewis Dartnell
Teacher package: Maths and art contains many fascinating links and articles
Getting Started
To get you started on the algebra, it might help to note that the mathematical curves used to represent Mondrian were
$$
\begin{eqnarray}
y&=&0.5\tan(1.2(x-1)) - 0.3\\
0.5(y-1.5)^2+x^2 &=& 0.6\\
(y-1.6)^2+0.25(x\pm 0.3)^2&=& 0.01\\
y&=&-8(x-1)^3\\
y&=&-2x-2\\
y&=&-4x -2\\
y&=&5x-2 \\
y&=&3x-2
\end{eqnarray}
$$
Teachers' Resources
Why do this problem?
This problem gives an engaging opportunity for genuine cross-curricular work whilst bringing in ideas from composition and transformation of functions. It forms the basis of the ideas underlying Computer Generated Images which are of fundamental importance in the gaming industry, into which many students might go.Possible approach
Find some images of
interest and discuss ways in which they might be
mathematised.
There are three levels of
possibility:
1) Look at the images and
discuss how they might by represented by standard mathematical
shapes.
2) Decide how the
outlines of key regions of the images might be represented by
mathematical curves.
3) Use graph paper or a
graphing package to start to quantify precisely the shapes or
curves: the goal is explicitly to find equations corresponding to
the key parts of the image.
You might suggest that
students are only allowed, say, 7 shapes or 7 curves with which to
represent the image. This will help to focus on the key aspects of
the images: the goal is to create a simple, abstract rendering of
the image.
You might also suggest
that students prepare the same images with their choices of
abstract curves and then ask someone from the art faculty to
determine which best represents the images.
Key questions
What are the key aspects
of the image?
Can you see any lines
which look like part of a standard function?
What is the equation of a
line / ellipse / parabola?
How do you make a curve
move left/right or up/down?
How do you stretch or
squash a curve?
Possible extension
Students can take this
task as far as they wish, in both the artistic or mathematical
directions. Suggestions for further reading are given at the foot
of the main problem.
Possible support
You could print off the
images and provide transparencies onto which the students could
draw as preparatory work.
If the equations of
curves' shapes are causing a problem, you might want to start with
straight lines and the problem Painting Between The
Lines.
