Overlaps
What does the overlap of these two shapes look like? Try picturing it in your head and then use some cut-out shapes to test your prediction.
Problem
If I have these two shapes:
and I overlap them a bit, I get this:
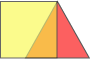
The overlapped part looks like this:
Can you match these pairs of shapes with the shape you would get if you overlapped them?
For accessibility: The first pair of shapes shows two squares. The second shows a square rotated, so that it is 'balancing' upright on its corner, and a rectangle. The third pair of shapes shows 2 rectangles with their shorter side as their base. The fourth pair of shapes shows 2 rectangles standing on their longer side as their base. The fifth pair of shapes shows 2 squares, one of which is upright and the other of which is 'balancing' upright on its corner. The sixth pair of shapes shows 2 triangles, one of which is upright and the other of which is 'balancing' upright on its corner.
The possible overlap shapes are a right isosceles triangle with its right-angled corner pointing right, a longer rectangle, a shorter rectangle, a parallelogram, a square, and a right isosceles triangle with its right-angled corner pointing left.
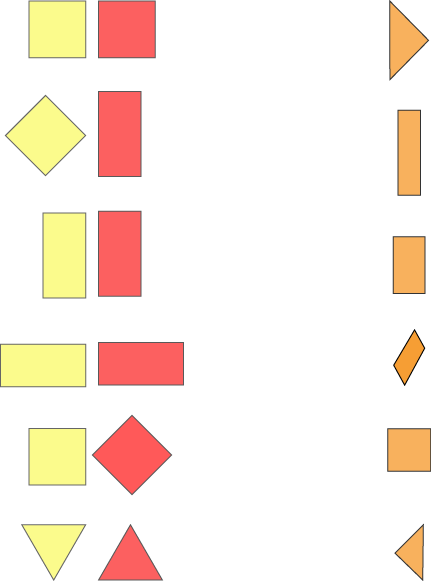
How did you work these out?
What other interesting overlap shapes can you make using a square, a rectangle and an equilateral triangle?
Getting Started
Try to "see" one shape moving over the other in your mind.
You could cut out the shapes in two different colours of tissue paper or cut up two overhead transparencies to test out your ideas. Or, you could try drawing the two shapes overlapping.
Student Solutions
We had just two submissions for this challenge, with pictures showing what they found.
Yihang from Wembdom St George sent in this picture:
Lily from St. Kevin's Geebung in Australia sent in four pictures, the first shows her answers and the next three shows where she went with successfully exploring other shapes.
Larger versions of those three are worth a look here.
Well done the two of you, maybe others will feel they want to explore further.
Teachers' Resources
Overlaps
If I have these two shapes:
and I overlap them a bit, I get this:
The overlapped part looks like this:
Can you match these pairs of shapes with the shape you would get if you overlapped them?
What other interesting overlap shapes can you make using a square, a rectangle and an equilateral triangle?
Why do this problem?
The main aim of this problem is to encourage children to try to picture images in their heads and to show that the image may be a dynamic one. The context of overlaps is likely to be new to them, which will hopefully peak their curiosity and inspire them to explore. As they work, they will be applying knowledge of properties of shapes, and using language associated with 2D geometry.
Visualising is a skill which can be invaluable in solving problems, and this problem provides an unusual context for practising it.
Possible approach
Rather than showing the image of the equilateral triangle overlapping the square in the first part of this problem, you could just show the image of the two separate shapes. Ask children to shut their eyes and imagine the triangle moving over the square. This will give them time to really focus on their own image, rather than being presented with someone else's straight away. Invite them to talk to a partner about what they can see in their mind's eye - what shape is the overlap? - and then talk about it as a whole group.
At this point, you could then show the image on screen or use shapes cut out of differently coloured transparent plastic sheets, or plastic wallets/folders. You could then ask the class to work on the problem in pairs, perhaps using cut-out shapes to test their hypotheses. (When working in small groups or pairs, shapes cut from tissue paper could be useful.)
Key questions
Tell me about how you are working on the problem.
Looking at the overlap, does its shape give you clues about which shapes made it?
Possible extension
Learners could try this more complex version of this problem.
Possible support
Suggest cutting out the shapes from this sheet and drawing round them to make overlaps.