Overarch 2
Bricks are 20cm long and 10cm high. How high could an arch be built
without mortar on a flat horizontal surface, to overhang by 1
metre? How big an overhang is it possible to make like this?
Problem
Image

Bricks are 20cm long and 10cm high. If you built a tower of single bricks without using mortar on a flat horizontal surface, how tall would the tower have to be for it to overhang by 1 metre? How big an overhang is it possible to make like this?
Getting Started
Student Solutions
Bricklayers build from the ground up,
but to solve this problem you must start at the top!
Alexander Maryanovsky
sent in a correct solution.
Let's adopt a unit of length of half the length of a brick,
and W as the weight of 1 brick.
|
Image

|
We want to calculate the formula for the overhang $d_n$ of
brick $n$ over brick $(n+1)$. (See the diagram). The idea is to
imagine inserting brick $n$ under the existing pile of bricks 1, 2,
3...$(n-1)$ (numbering the bricks from the top) so that the centre
of mass of bricks 1, 2, 3... $(n-1)$ will be exactly above the edge
of brick $n$. You can treat the edge of brick $(n+1)$ as the fulcrum of a balance. The maximal arch will be created when there is a perfect balance on each edge. |
Image
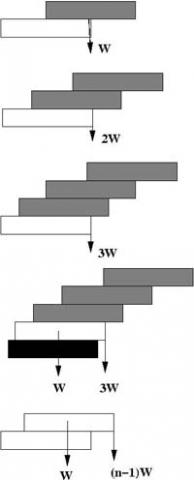
|
If you calculate $d_1$, $d_2$,... you should find that
\begin{eqnarray} d_1 &=& 1\\ d_2
&=& {1\over 2}\\ d_3 &=& {1\over 3}\\
\end{eqnarray}
So it seems likely that $d_n = {1\over n}$.As the centre of mass of the stack of bricks above must be
exactly over the edge of the next brick down, we take moments for
the stack of $n$ bricks resting on the $(n+1)$st brick (counting
the bricks from the top). We need the centre of mass of (n-1)
bricks at distance $d_n$ from the fulcrum to balance 1 brick (the
$n$th brick) at distance $(1 - d_n)$. Hence \begin{eqnarray} W(1 -
d_n) &=& (n-1)Wd_n\\ d_n &=& {1\over n}
\end{eqnarray} The total overhang $A_n$ for an arch containing $n +
1$ bricks is therefore $$ A_n = \sum_1^n 1/n $$
|
Alexander went on to say...
After some asking around, I was told there is no closed form for that. A small computer program that looks like this:
double overhang = 0;returns 12367 as the number of bricks needed to make an overhang of 1m, making its height 12367*10cm = 1,236.7m Since 1+1/2+1/3+...+1/n doesn't converge, you can make the overhang as big as you wish (I'm not gonna go into counting how much material for those bricks is needed and if there's enough of it in the universe :-) )
double brickWidth = 20;
double maxOverhang = 100;
double numBricks = 0;
while (overhang < maxOverhang){
numBricks = numBricks+1;
overhang = overhang+brickWidth/(2*numBricks);
}
Teachers' Resources
Why do this problem?
This is such a surprising result that one would hope it would intrigue and motivate students to learn more mechanics. It also links to the harmonic series and ideas in pure mathematics. The proof depends on the simple idea of taking moments about a fulcrum.
After the students have done the problem, it is enlightening to discuss the fact that in practice, the building plan has to be made knowing the total of all the overhanging distances first and hence, from the harmonic series, the number of bricks required. This is because, suppose $(n+1)$ bricks are required, the overhang of the first brick to be put in place has to be ${1\over n}$ and the overhang of the topbrick ${1\over 2}$ a brick length.
Possible approach
How about doing some calculations and then building your own structures using dominoes or Jenga pieces? You might challenge the students to build 2 symmetric arches meeting at the top with 10 dominoes and the width at the bottom slightly more than two domino lengths.
As with many problems it is advisable to start with simple cases (here 2 bricks then 3, then 4) and then to make a conjecture about the general result. It is somewhat counter-intuitive to work from the top down but this is inherent in working through these simple cases.
Numbering the bricks from the top down, to achieve the maximum overhang, the $(n-1)$ bricks on top of brick n have centre of mass exactly above the edge of brick $n$, and then we need to take moments about a fulcrum at the edge of the $(n+1)$st brick.
Key question
What forces act on brick $n$ if it balances on a fulcrum at the end of the brick below it?
What is the total number of bricks needed for the top brick to be nowhere vertically above the bottom brick? (Answer: 5 bricks.)
Possible support
Try the problem Overarch 1
Possible extension
Try the problem Harmonically.
Note how the proof that the harmonic series is divergent relates to the second key qestion above. This can be extended to ask how many bricks (roughly) would you use to be certain of getting a total overhang of two brick lengths, then 3, then 4.... giving the number of terms in the partitions of the series in the proof of divergence. However this eventually overestimates the number needed, the divergence proof being based on inequalities. The overarch answers depend on $\log n$ whereas the partial sums in the estimate depend on $\log 2$.
