Orthogonal circle

Given any three non intersecting circles in the plane find another circle or straight line which cuts all three circles orthogonally.

Age

16 to 18

Challenge level

Being curious Being resourceful Being resilient Being collaborative

Problem

A large circle orthogonal to three other circles. One intersection is marked B and the two respective centres of the circles are marked B and C. A, B, C form a right-angled triangle.

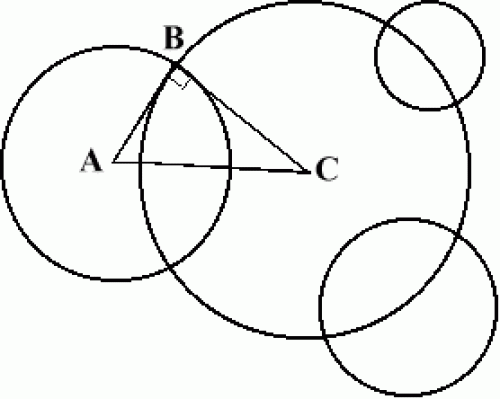
It is known that given any three non intersecting circles in the plane there is another circle or straight line that cuts the three given circles at right angles. (The circle or straight line is said to be orthogonal to the 3 original circles.)

Given three circles with centres $(0, 0)$, $(3, 0)$ and $(9, 2)$ and radii $5$, $4$ and $6$ respectively find the centre and radius of the circle that cuts the three given circles at right angles. Draw the circles to check that the circle you have found appears to be orthogonal to the others.

What happens in the case of three circles with centres at $(0, 0)$, $(3, 3)$ and $(8, 8)$ and radii $1$, $2$ and $3$ respectively?

Given three circles, how can you tell without calculating which of the two cases applies, an orthogonal circle or an orthogonal straight line?

Student Solutions

set var="TeX" value="l2h"

Congratulations to Tony from State College Area High School, Pennsylvania, USA for this solution.

First of all, here is the solution to finding the equation of the orthogonal circle for the circles with centers of $(0,0)$, $(3,0)$, $(9,2)$ and radii respectively of $5$, $4$, and $6$.

As the circles are orthogonal we can draw three right angled triangles. One of the legs of each right triangle is the radius of one of the given circles, the other leg is the radius of the unknown orthogonal circle, and the hypotenuse is the distance between the center of the known circle and the center of the unknown orthogonal circle.

Since we have three given circles, we can use the Pythagorean Theorem three times to find our answer. Here are the equations that find the center (h,k) of the orthogonal circle with radius r:

$\begin {eqnarray} 5^2 + r^2 &= h^2 + k^2 \quad (A) \\ 4^2 + r^2 &= (h-3)^2 + k^2 \quad (B) \\ 6^2 + r^2 &= (h-9)^2 + (k-2)^2 \quad (C) \\ \end {eqnarray}$

Now subtract equation (B) from equation (A) to get $18 = 6h$, so $h=3$. Now plug $h=3$ in equation (A) to get $r^2 + 16 = k^2.$ Next plug $h=3$ and $k^2 = r^2 + 16$ into equation (C) to get :

\[r^2 + 36 = (-6)^2 + (r^2 + 16) -4k + 4\]

from which we find $k = 5.$ Plug $k=5$ in equation (A) to get $r=3.$ So now we have all we need to make the equation of the orthogonal circle: $h=3$, $k=5$ and $r=3$, so the equation of the orthogonal circle is $(x-3)^2 + (y-5)^2=9.$

When we try to find the orthogonal circle for the second example, we end up with simultaneous equations which are fruitless, unsolvable. This means the second equation has an orthogonal line, in this case a fairly obviously one with $y=x.$

Now I will prove that you have an orthogonal line when the centers of the circles are collinear, otherwise you have an orthogonal circle.

Any orthogonal line would have to form a right angle with every given circle. When a line forms a right angle with the circumference of the circle, that means it passes through the center of the circle, so our orthogonal line passes through the centers of all the circles. The only way this is possible for our line to accomplish this (since two points determine a line, three points determine a plane), is if all three centers are collinear.

Therefore, lines can handle every case of collinear centers, and since an orthogonal line or circle can always be drawn, every other case is covered by an orthogonal circle.

[We have used Tony's American spelling of center here. Ed.]

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Orthogonal circle

Problem

Getting Started

Student Solutions

Teachers' Resources