Multiply the Addition Square
If you take a three by three square on a 1-10 addition square and
multiply the diagonally opposite numbers together, what is the
difference between these products. Why?
Age
11 to 14
Challenge level
Problem
Take an addition table from $1$ to $10$ (or any other that you like better!):
Image
Now take a $3\times 3$ square of numbers on it, such as this
red one:
Image
Now multiply the two diagonally
opposite corner numbers together:
Image
And then find the difference between the two answers:
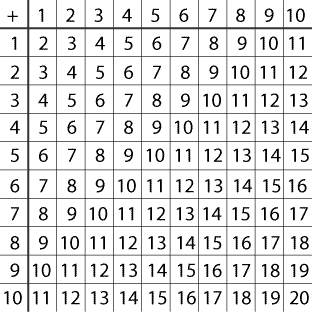
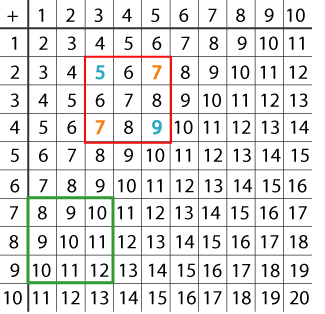
$5 \times 9 = 45$
$7 \times 7 = 49$
$49 - 45 = 4$
Now try the numbers in the green
square:
Image
What is the answer?
Investigate other $3\times 3$ squares.
What do you notice?
Can you explain it?
Now try with $2\times 2$ squares and $4\times 4$
squares.
Can you predict your answers? What is happening?
Getting Started
How do the four numbers compare in size?
Try comparing the number in the top left corner of a square with the other three numbers.
So what happens when these numbers are multiplied in the way described?
You may like to print off this addition square to try out your ideas.
Student Solutions
Mr Skipper (who didn't send us his first name) was the first to send in a solution:
Wherever we place the square, the number in the top left corner is the smallest.Call this $n$.
The arbitrary square becomesn n+1 n+2
n+1 n+2 n+3
n+2 n+3 n+4
So the product of the top left and bottom right is
n(n+4) = n^2 + 4n.
The product of the top right and bottom left is
(n+2)^2 = n^2 + 4n + 4.(n^2 + 4n + 4) - (n^2 + 4n) = 4.
So the difference is always 4.
Annette aged 13 did really well and generalised the problem still further. She considered what would happen if you had any sized square on the same addition grid.
Annette talks about the size of the square to be N by N, and the first number in the top left of the square to be k.
For an N x N square, the difference is -(N-1)*(N-1),
since k=number in top left then
k(k+2N-2)-(k+N-1)*(k+N-1)= -(N-1)*(N-1),
Teachers' Resources
Why do this problem?
This problem is a good one for building on the learners' ability to recognise number properties and reason about numbers. It is easy for all at the start as it only requires simple multiplication and subtraction and gives the satisfaction of finding a pattern. If the results are generalised algebraically it can prove a real challenge.Possible approach
You could start by posing the problem to the whole group on a
computer or using a large-sized addition square.
After this learners could work in pairs on the problem so that
they are able to talk through their ideas with a partner. This
sheet gives two copies of the addition square which can be used for
rough work.
Many learners will tend to rush on and try $2 \times 2$, $4
\times 4$ and other squares and although an interesting pattern can
be found doing this, it may stop them from trying to generalise the
$3 \times 3$ example. Therefore, it may be wise to stop everyone at
an appropriate point and show all who need the help how the numbers
can always be named $n, n + 2$ and $n + 4$. (Alternatively, they
could be $n - 2$, $n$ and $n + 2$.)
At the end of the lesson learners could discuss the different
patterns they have discovered and the various generalisations
made.
Key questions
How do the four numbers compare in size?
Try comparing the number in the top left corner of a square
with the other three numbers.
So what happens when these numbers are multiplied in the way
described?
Can you see a pattern there?
What sort of numbers are these?