Month mania
Problem
When it's the end of January and we need to turn over a page of our calendar, the next page may look a bit like this:
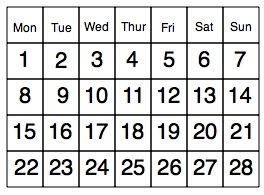
Of course, it probably has a good picture on the page as well, perhaps of a scene from a T.V. show or an animal from your favourite story book.
If we ignore the edge squares which tell you what day of the week it is, then we have a rectangle with twenty eight squares in it like this:-
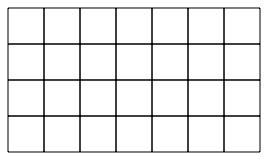
Well, how about going a bit wild and designing a new shape for these twenty eight squares in which the numbers follow on in some way that is not too difficult to follow? For example, you could put the twenty eight squares into a triangle and decide to go in an up-and-down order like this:-
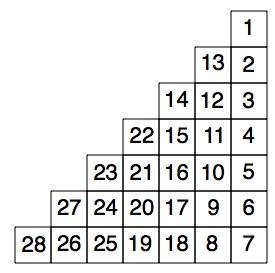
What other wonderful designs can you come up with?
You can then go further by looking at the way the numbers are arranged and see if you can spot any patterns. For example in the first usual way:-
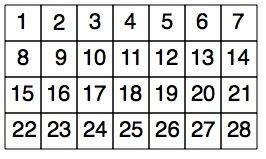
you may notice things like:
1. If you take any two by two square (like the one in at the top left-hand corner with $1$, $2$, $8$ and $9$ in it), then the opposite corners of that square add up to $10$. Then, if you take the next two by two square along [with $3$, $4$, $10$ and $11$ in] then the opposite corners add up to $14$ and so on.
2. Going down any column the numbers increase by $7$.
Do let us know what you discover in the designs you have created. Can you explain why the patterns occur?
Then ask "I wonder what would happen if ...?''
Getting Started
Try using squared paper to explore the possible arrangements of the squares and numbers.
Student Solutions
John from St. Edburg's wrote;
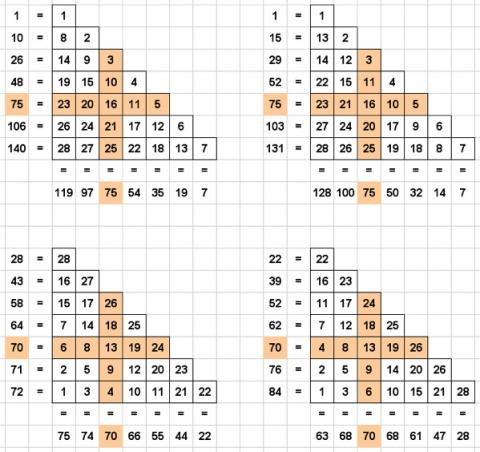
TOP LEFTI made the numbers into a triangle, starting in the top corner. When I got to the bottom I started again at the top. I noticed that the middle row and the middle column both added up to $75$.
TOP RIGHT
I wondered what would happen if I went down, then up, then down again in a zigzag instead of just filling in the numbers downwards. I had no idea that the middle row and the middle column were going to add up to $75$ again!
BOTTOM LEFT and BOTTOM RIGHT
I tried putting the numbers in a different order again, starting in the bottom left hand corner. In the bottom left picture I did the same zigzag as in the top right, and in the bottom right picture the numbers are filled in diagonally from top to bottom. I wondered if the middle row and middle column would add up to $75$ again, but they didn't. They all added up to $70$!
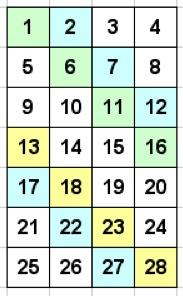
When I put the numbers into this grid, I spotted that on diagonal rows the units repeat. This is because each number down the diagonals is $5$ higher than the one before it ($1, 6, 11, 16$ and $13, 18, 23, 28$).
Well done this was really a good investigation for you - keep going !
Teachers' Resources
Month Mania
When it's the end of January and we need to turn over a page of our calendar, the next page may look a bit like this:
Of course, it probably has a good picture on the page as well, perhaps of a scene from a T.V. show or an animal from your favourite story book.
If we ignore the edge squares which tell you what day of the week it is, then we have a rectangle with twenty eight squares in it like this:-
Well, how about going a bit wild and designing a new shape for these twenty eight squares in which the numbers follow on in some way that is not too difficult to follow? For example, you could put the twenty eight squares into a triangle and decide to go in an up-and-down order like this:-
What other wonderful designs can you come up with?
You can then go further by looking at the way the numbers are arranged and see if you can spot any patterns. For example in the first usual way:-
you may notice things like:
1. If you take any two by two square (like the one in at the top left-hand corner with $1$, $2$, $8$ and $9$ in it), then the opposite corners of that square add up to $10$. Then, if you take the next two by two square along [with $3$, $4$, $10$ and $11$ in] then the opposite corners add up to $14$ and so on.
2. Going down any column the numbers increase by $7$.
Do let us know what you discover in the designs you have created. Can you explain why the patterns occur?
Then ask "I wonder what would happen if ...?''
Why do this problem?
Possible approach
You could then give them all a piece of $1$ cm squared paper and suggest they explore different arrangements of the twenty eight squares with the numbers arranged in some logical order. In the same way, they can look for any patterns of numbers that appear. If they work in pairs they will be able to talk through their ideas with a partner.