Mean Geometrically
A and B are two points on a circle centre O. Tangents at A and B cut at C. CO cuts the circle at D. What is the relationship between areas of ADBO, ABO and ACBO?
Age
16 to 18
Challenge level
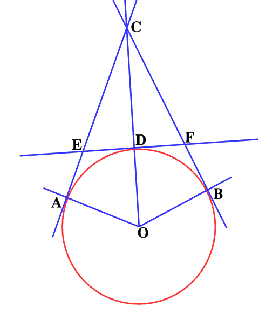
$O$ is the centre of a circle with $A$ and $B$ two points NOT on a diameter. The tangents to $A$ and $B$ intersect at $C$. $CO$ cuts the circle at $D$ and a tangent through $D$ cuts $AC$ and $BC$ at $E$ and $F$.
What is the relationship between area of $ADBO$ and the areas of $ABO$ and $ACBO$?
Area fomulas and a little trig will help.
Here is the diagram if you need some clues to get started:
Image
Image
|
This involves nothing more than areas of right angled
triangles, using the symmetry in the diagram, and sines, cos's and
tan's.
Well done M.S. Ezzeri Esa from Cambridge Tutors College,
Croydon and thank you for this solution.
Let radius = $r$; $\angle AOD = \angle BOD = \alpha$
Area $ADBO$ = $2 ({1\over 2 }r^2 \sin \alpha) = r^2 \sin
\alpha$
Area $ABO$ = ${1\over 2}r^2 \sin 2\alpha = r^2 \sin \alpha
\cos \alpha$
Area $ACBO$ = $2({1\over 2}r^2 \tan \alpha) = r^2 \tan
\alpha$
(Area $ABO$). (Area $ACBO$) = $r^2 \sin \alpha \cos \alpha\ .\
r^2 \tan \alpha = r^4 \sin^2 \alpha ={\rm (Area ADBO)}^2.$
The area of $ADBO$ is the geometric mean of the areas of $ABO$
and $ACBO$
|