Making Sixty
Why does this fold create an angle of sixty degrees?
Problem
Take a piece of paper.

Fold it along the long axis and then open it up.

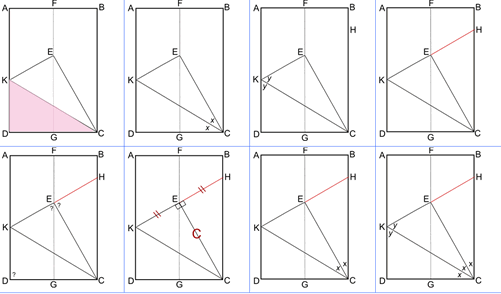
Now fold one corner over and onto the centre crease so that the fold line passes through the corner next to it (on the short side of the paper).
You have created some angles. There are angles of $60^o$ and of $30^o$. Can you prove this?
Does the paper have to be A4?
You are now able to fold the paper to make an equilateral triangle which can be used in lots of different ways. For example, see Equilateral Triangle Folding .
Getting Started

Student Solutions
Congratulations to all those who submitted solutions. Billy from Sedgehill School drew a diagram showing sides and angles he knew must be equal, which helped him to spot 30 and 60 degree angles. Patrick from Woodbridge School went a little further and made a good argument using ideas about congruent triangles. Jack's (Fast Forward) solution was also very clear and used similar ideas to Patrick's; I have combined their solutions below.

I know that KEC is a right angle because it is the corner of the paper, so as KH is a straight line, CEH is also a right angle. The line KE = EH; I know this because E lies on FG which divides the sheet in two. EC is common to both triangles, so triangles KEC and CEH are congruent (Side-Angle-Side).
I know that triangle KDC is also congruent to KEC because we folded corner D up to E to create the two triangles.
As the three triangles are congruent, I know that angles DCK, KCE and ECH are all equal, so as DCH is a right angle, each angle must be $90 \div 3$ which is $30$ degrees.
Angles in a triangle add up to $180$ degrees, so angle CKE and CHE are $180-90-30=60$ degrees, so triangle CKH is equilateral.
Teachers' Resources
Why do this problem
This problem involves a simple construction which gives a surprising and useful result. Having confirmed the sizes of angles this knowledge can be applied to make images and polyhedra. Different routes to solution can also lead to useful discussions, including how well learners explain their reasoning and the elegance of their methods.
Possible approach

Key questions
What side lengths or angles do you know?
Possible support
Spending time making triangles and feeling confident about their properties is a useful starting point. Finding triangles that might be congruent, cutting them out and testing the congruency by matching them can then lead to identifying why sides and angles might be equal.
Possible extension
See:
Paper Folding - Models of the Platonic Solids.
Can learners justify all the results used as they work?
