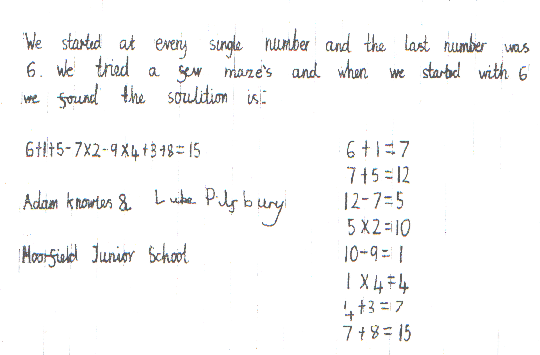A-magical number maze
The rows, columns and main diagonals of a $1$ - $9$ magic square add to the same number, $15$.
This magic square has had doors, with operations written in them, opened to make it into a maze.
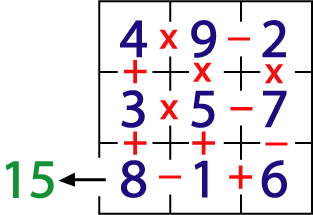
Start wherever you like and go through every cell using all the numbers, doing the operation indicated to the numbers, and go out through the exit marked in cell $8$ with a total of $15$!
You must use the operations and numbers strictly in the order you meet them. For example, if you try starting at $4$ and go across the top row you must do it like this:
$4\times 9 = 36$
$36 - 2 = 34$
NOT like this:
$4 \times (9 -2) = 4 \times 7 =28$
Remember to use every number in your route round the maze.
Keep a record so you know whether you have tried that route before or not.
You might find it useful to print out this sheet which has twelve copies of the maze.
Joe from St Aldhelm's School has found one way through the maze:
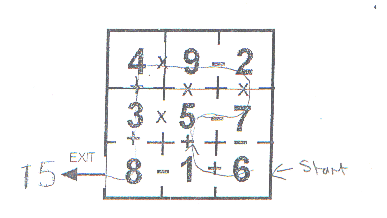
Is there any other route that works? Remember you must use every number. How can you check to see if you have found all the possible routes?
Adam and Luke from Moorfield Junior School tried starting at every number before they tried the six! Here is their solution:
