Magic Caterpillars
Problem
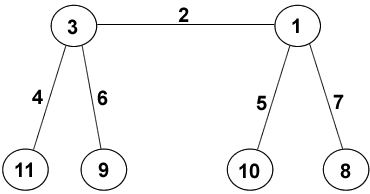
In the Land of Trees all the caterpillars have numbers on their feet and hips (vertices) and on their legs and body segments (edges) as shown on this 4 legged caterpillar. All the whole numbers from 1 to $v+e$ are used where $v$ is the number of vertices and $e$ is the number of edges. Biologists classify them by their vertex-sums.
A vertex sum is the total of the numbers on the vertex and all the edges at that vertex.
The caterpillar shown has vertex sums:
11 (8+3), 13 (9+4), 15 (10+5), 17 (11+6), 25 (8+9+7+1) and 30 (7+10+11+2).
Show that one day a biologist may find a rare magic 4-legged caterpillar having the same sum at all its vertices and describe this creature.
Could there be two species of magic 4-legged caterpillars with different numberings?
Do magic 6-legged caterpillars exist?
What about magic caterpillars with even more legs?
Getting Started
The numbers on the edges are counted twice.
The reasoning needed here is much the same as for the problem Plum Tree. See the detailed hint for Plum Tree.
Student Solutions
Peter sent us this solution, using the starting point we gave:
There are $6$ vertices and $5$ edges. Let's suppose the magic constant is $S$ and this is the same at each vertex. The total of all the numbers $1 + 2 + ... + 11 = 66$ but the numbers on the edges, $a,b,c,d,e$ are counted twice. So, adding the magic sum at all six vertices:
$$(a+b+c+d+e)+66=6S$$
So $a+b+c+d+e$ is a multiple of $6$ and it is at least $1+2+3+4+5=15$ so it must be $18$ or more. Hence $6S\geq84$ and $S\geq14$.
We're going to call the horizontal edge $e$, the front two edges $a$ and $b$, and the back two legs $c$ and $d$. Also, we see that the numbers $11$, $10$ and $9$ must all be in feet, as they're too big to be anywhere else.
Let's try $S=14$ first. We may as well take $a=3$, as the legs are all interchangeable at this stage.
Now if $b=4$, then we have $c=5$ (as the back legs are interchangeable). Also, we must have $d$ and the back foot as $6$ and $8$ (in some order), and we soon see that this isn't possible (as we'd also need $e$ plus the top left hip to add up to $7$). If $b$ isn't $4$, then we can assume that $c=4$. But similarly we find that we can't have $b=9$ or $b=8$ or $b=7$. So $S$ isn't $14$.
Let's try $S=16$. But then we need four pairs of numbers that sum to $16$ (one for each leg). We try: $(11,5)$, $(10,6)$, $(9,7)$, $(8,?)$ and we can't repeat the $8$ so that isn't possible.
So let's try $S=15$. This time, we may as well take $a=4$. There are only $4$ pairs that add up to $15$: $(11,4)$, $(10,5)$, $(9,6)$ and $(8,7)$. Call the number in the top left hip $f$.
If $b=5$, then we have $c=6$ and $e+f=6$, which isn't possible (as we don't have the right numbers left).
So we can take $c=5$. If $b=8$, have $e+f=3$ and then we'll need $f+g=4$, and this isn't possible. If $b=7$, have $e+f=4$ and we also have $f+g=4$ and this isn't possible either. Also we can't have $d=8$, as this is too big. So the only possibility is the one shown below (and this does indeed work).
(When I say the only possibility, of course the front legs could be switched, or the back legs, or the front and back swapped, but it's really the same caterpillar.)