Lost in Space

How many ways are there to count 1 - 2 - 3 in the array of triangular numbers? What happens with larger arrays? Can you predict for any size array?

Age

14 to 16

Challenge level

Exploring and noticing Working systematically Conjecturing and generalising Visualising and representing Reasoning, convincing and proving

Being curious Being resourceful Being resilient Being collaborative

There are three ways to enter the triangular array of numbers in the diagram below, starting with 1, and counting from 1 -2 in order, finishing with the two in the bottom row.

How many ways are there to count 1 - 2 - 3 in the following array?

And 1 - 2- 3 - 4 on this?

Can you generalize?

Can you explain what you find?

Derek (no school given) offered the following insights into this problem: - and nicely explained too - thank you Derek.

From observation, we compile the table below:

n-row pyramid	Ways to count 1-2-3-...
1	1
2	3
3	7
4	15
...	...

The pattern can be deduced by considering route backwards, i.e. from n back to 1. The general n-row pyramid is shown below:

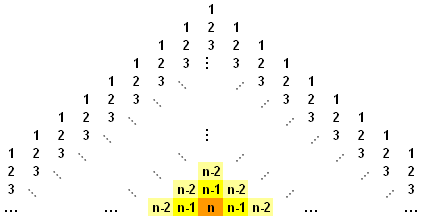
Starting at the orange square, we assert that there are 0 routes leading to the final square:

1 step earlier, at the bright yellow squares, there is 1 route leading to the final square:

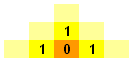
1 step earlier, at the light yellow squares, the situation becomes slightly different.The top, left and right squares all have 1 route leading to the final square. However, the middle squares have 2 routes as they each connect to 2 bright yellow squares (each of which are routes leading to the final square):

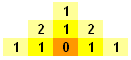
1 step earlier, the top, left and right squares all have 1 route whilst the middle squares have 3 routes as they each connect to 2 light yellow squares, bearing a total of 3 routes. We repeat this reasoning and get the following pattern:

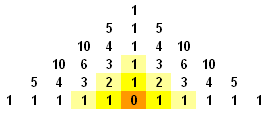
It is clear that these are the binomial coefficients. 2 of Pascal's triangles have been arranged together and the numbers along the two slanted edges represent how many ways to count 1-2-3-...-n. For example, in the diagram of the 6-row pyramid above, we see that there are 1+5+10+10+5+1+5+10+10+5+1 = 63 ways to count 1-2-3-4-5-6.

We further notice that 1, 5, 10, 10, 5, 1 are the binomial coefficients $5 \choose {k}$ $,k = 1, 2, 3, \cdots, 5 $. We generalise by claiming that the number of ways of counting $1-2-3-...-n$ is twice (because there are two Pascal's triangles) the sum of all the binomial coefficients of the $n-1^{th}$ row minus 1 (because of the overlapped 1 down the central column) which can be written as $2\sum_{k=0}^{n-1}$ ${n-1}\choose{k}$ $ - 1$.

Editor's comment: at this point it may be worth mentioniing that the sum of the binomial coefficients are powers of 2. Why?

Chen of the Chinese High School took a slightly different approach (similar to the one offered by Andrei of Tudor Vianu National College):

We shall define $T(n)$ to be the number of ways to count 1 - n in a triangular array of 1 - n. We shall solve this problem by establishing a recurrence relation, and hence finding a formula for $T(n)$.

When $n=1, T(1)=1$ and when $ n=2, T(2)=3$. We observe that in a triangular array of 1-3, the number of ways to get to the number '2' directly above the number '3' is given by $T(2)$ and the number of ways to get to the '2' on the left of '3' can be easily computed to be 2.

Similarly, there are 2 ways to get to the '2' on the right of the '3'.

Hence, $T(3)=T(2)+2^2=7$ For $T(4)$, we observe again that the number of ways to get to the '3' directly above of the '4' is given to be $T(3)$.

Furthermore, the number of ways to get to the '3' to the left of the '4' is the sum of the number of ways to get to the '2's adjacent to the '3'.

Since by the previous result, there are 2 ways of getting to the '2', there are 2+2=4 ways of getting to the '3' to the left of the '4', and similarly for the '3' to the right of the '4'. Hence, $T(4)=T(3)+2(2^2)=T(3)+2^3$ Extending this argument to T(n), we obtain the recurrence $T(n)=T(n-1)+2^{(n-1)}$.

However, since $T(n-1)=T(n-2)+2^{(n-2)}$, which is also equal to $T(n-3)+2^{(n-3)}+2^{(n-2)}$.

Thus, it is not difficult to see that $T(n)= 1+2+2^2+2^3+...+2^{(n-1)} or 2^n - 1$

Editor's comment: The final result can be verified by summing the geometric series with first term 1 and common ratio 2. You can test your understanding of this proof using the proof sorter at http://www.nrich.maths.org/public/viewer.php?obj_id=1398.

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Lost in Space