Linkage
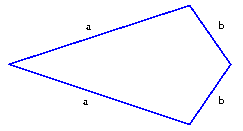
Four rods, two of length a and two of length b, are linked to form a kite, as shown in the diagram. The linkage is moveable so that the angles change. What is the maximum area of the kite?
Now suppose the four rods are assembled into a linkage which makes a parallelogram. What is the maximum area of this parallelogram?
Congratulations Christian,Nisha and Suzann, The Mount School York for seeing just how simple this problem really is - just two right angled triangles. Well done also to Sarah and Alice from the same school; they used 'half ab sin C ' but 'half base times height' is really all that is needed.
The kite is made up of two triangles if we divide it along it's axis of symmetry.
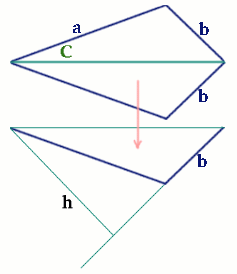
If we call b the base of the triangle then its maximum height has got to be a , see the diagram below.
The area of this triangle is:
|
and h will always be smaller than a as a is the hypotenuse of the right-angled triangle made up of the green lines and side a .
The maximum value of the area of the triangle will be when h = a , so the maximum area of the triangle is :
|
and the area of the kite will just be b x a
If the rods are made into a parallelogram it won't change things because the parallelogram is made up of the same two triangles as the kite.
This means that the parallelogram of maximal area is actually a rectangle, well done!