The lily pond
Problem
Once there was a rectangular lily pond. In it there were $12$ lily leaves and $6$ lily flowers.
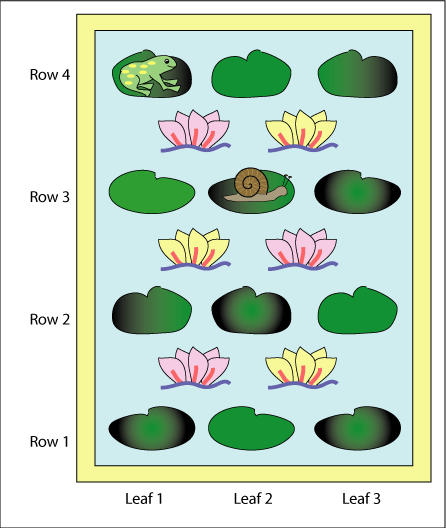
Freddie the Frog lived on one lily leaf which we will call "leaf $1$, row $4$". Sammy Snail lived on another leaf which we will call "leaf $2$, row $3$". Freddie used to jump from leaf to leaf but he did not like jumping over the lily flowers so he never jumped diagonally.
One day Freddie went to see Sammy Snail. He visited as many of the leaves as he could on the way but only visited each leaf once. Which was the best way for him to go?
If Sammy lived on a different leaf Freddie would be able to go on every leaf on his way to see Sammy. Which leaves would make this possible?
Getting Started
Student Solutions
Alistair explains how Freddie the Frog jumps:
- First of all, Freddie Frog hops to
- Row 3, Leaf 1 then to
- Row 2, Leaf 1 then to
- Row 1, Leaf 1 then to
- Row 1, Leaf 2 then to
- Row 1, Leaf 3 then to
- Row 2, Leaf 3 then to
- Row 3, Leaf 3 then to
- Row 4, Leaf 3 then to
- Row 4, Leaf 2 then to
- Row 3, Leaf 3 to meet Sammy Snail.
Including the first leaf, Freddie has hopped on 11 leaves. He missed out Row 2, Leaf 2.
There is also another way to get to Sammy Snail that includes Row 2, Leaf 2, but it misses out a few more leaves.
Alistair goes on to say:
Freddie could jump on all the leaves if Sammy lived on
- Row 1, Leaf 3, or if she lived on
- Row 2, Leaf 2 or
- Row 3, Leaf 3, or
- Row 1, Leaf 1.
Alistair tells us that his mum thinks there is another place too. What do you think?
Teachers' Resources
The Lily Pond
Once there was a rectangular lily pond. In it there were $12$ lily leaves and $6$ lily flowers.
Freddie the Frog lived on one lily leaf which we will call "leaf $1$, row $4$". Sammy Snail lived on another leaf which we will call "leaf $2$, row $3$". Freddie used to jump from leaf to leaf but he did not like jumping over the lily flowers so he never jumped diagonally.
One day Freddie went to see Sammy Snail. He visited as many of the leaves as he could on the way but only visited each leaf once. Which was the best way for him to go?
If Sammy lived on a different leaf Freddie would be able to go on every leaf on his way to see Sammy. Which leaves would make this possible?