Ladder and cube

A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?

Age

14 to 16

Challenge level

Secondary

GEOMETRY

Pythagoras' Theorem & Trigonometry

Being curious Being resourceful Being resilient Being collaborative

Problem

Ladder and Cube printable sheet

A cube (1 metre by 1 metre by 1 metre) has one face on the ground and one face pushed up against a wall.

A 4 metre long ladder is leaning against the wall, just touching the cube.

A unit cube resting against a wall and the floor. A ladder is placed so that it is on the floor, touching the edge of the cube which is opposite the edge touching both the floor and wall, and the ladder is also touching the wall.

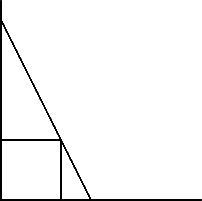
How high is the top of the ladder above the ground?

Student Solutions

This solution is by Anthony of Prince Henry's High School, Evesham. Well done Anthony.

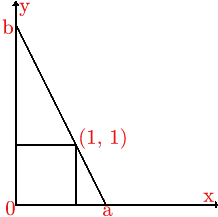
I viewed the ladder as a line, cutting the $x$ axis at $x = a$ and the $y$ axis at $y = b$, passing through the point $(1,1)$ with $a$ and $b$ such that $a^2 + b^2 = 16$ by Pythagoras theorem. The gradient of the line is $- b/a$ (the change in $y$ divided by the change in $x$). As $a =\sqrt{16-b^2}$, the gradient is $\frac{-b}{\sqrt{16 - b^2}}.$ The equation of the line of the ladder is:

$$y = -\frac{b}{\sqrt{16 - b^2}}x + b.$$ When $x = 1, \ y = 1$ we have $$ 1 = \frac{-b}{\sqrt{16 - b^2}} + b$$ and hence $$b^4 - 2b^3 - 14b^2 + 32 b -16 = 0.$$

This can be solved using a numerical search method (such as interval halving) to give the approximate solutions $b = 1.36$ and $3.76$ (to $2$ decimal places). These are the two possible heights of the top of the ladder. In each case, if one value is the height of the top of the ladder, the other value is the distance of the foot of the ladder from the wall.

Alternatively, the gradient is $-b/a = (1 - b)/(1 - 0)$, hence $ab = a + b $. Using the fact that $a^2 + b^2 = 16$ this gives $$(ab)^2 = (a + b)^2 = a^2 + 2ab + b^2 = 16 + 2ab.$$ Hence $$(ab)^2 - 2ab - 16 = 0.$$ Solving this equation gives $ab = 1 \pm \sqrt{17}$. As $a$ and $b$ are positive the solution here is $ab = 1 + \sqrt {17}$. We are looking for $a$ and $b$ and we know the sum $a + b$ and the product $ab$ are both equal to $1 + \sqrt{17}$. We can write down a quadratic equation with these roots and solve it. Hence $a$ and $b$ are the roots of $$x^2 - (1 + \sqrt{17})x + (1 + \sqrt{17}) = 0.$$

Solving this equation using the quadratic formula gives the values $3.7609$ and $1.3622$ (to $4$ decimal places). There are two solutions, one with the ladder at a steeper angle (it turns out to be approximately $70$ degrees) and the other at approximately $20$ degrees.

Yet another method uses numerical approximation. Taking the angle of the ladder with the ground to be $\theta$, then $a = 4 \cos \theta$ and $b = 4 \sin \theta$. Set up a spreadsheet or a program to evaluate $ab - (a + b)$ and use an interval halving method to find value of $\theta$ for which $ab - (a + b)$ is close enough to zero to give the values of $a$ and $b$ to sufficient accuracy.

Teachers' Resources

Why do this problem?

This problem provides an opportunity to practise Pythagoras Theorem and solving three-dimensional geometric problems in a real-life context.

While this problem can be approached from various methods using similar shapes, trigonometry, or equations and gradients of a straight line, it also develops algebraic fluency and reasoning.

The problem yields an equation which students may not be able to solve, so there is an opportunity to explore it using graphing or spreadsheet software. Through this they can explore several different representations.

Possible approach

Start by asking students to draw a diagram to visualise the problem, and ask whether there is more than one position the ladder could be in. Then ask them to consider what they know is always true in this situation. If you want to encourage a coordinate geometry approach, you might want to label the floor and the wall as the x and y axes.

Then, you could let students guess the height, and check if their guess ‘works’. They could do this beginning from any other quantity, such as the distance between the foot of the ladder and the cube. Let them work in groups as they try out different numbers and develop a set of conditions that must be met, using Pythagoras’ Theorem and similar triangles. Circulate as they work, first encouraging them to record their results systematically and then to generalise: what happens if you guess that the height is $h$ metres?

Bring the group together to share their ideas. Several different sets of equations and/or expressions may have arisen, containing fractions and square roots. You might want to use graphs to represent the expressions. For example, the ‘gradient’ of the ladder is $\frac{h}{\sqrt{16-h^2}}$ and the ‘gradient’ of the triangle above the ladder is $h-1.$ You could plot these two expressions, or any similar expressions the students have come up with, by hand or using graphical software. You could also use a spreadsheet package like Excel to find solutions.

Alternatively, if you want to use a purely algebraic approach, you could ask students to identify lengths that are unknown but useful to work out the height of the ladder. You might allow students to label diagrams with their own choice of letters and to write down equations explaining the relationships between their letters. Different choices of unknowns and conditions result in different systems of simultaneous equations which all combine to give quartic polynomials. The neatest solution we’ve found (recorded in the student solutions) comes from setting the height of the top of the ladder and the distance of the foot of the ladder from the wall as unknowns.

Key questions

What quantities are fixed and what quantities are variable in this problem?

As the ladder is sliding against the wall, what is always true?

Are there any equal angles in the diagram so that we could find similar triangles and establish relationships between lengths of unknow segments?

Possible support

You could begin with the same situation, but with the height of the top of the ladder given and ask students to find the length of the ladder. Repeat this for a few different heights, and then introduce the problem.

Recap of similar triangles.

Recap of Pythagoras’ Theorem.

Possible extension

How high is the top of the ladder above the ground if the ladder is L meters long (or a different number)?

What is the angle between the ladder and the ground?

Or search by topic

Number and algebra

Geometry and measure

Probability and statistics

Working mathematically

Advanced mathematics

For younger learners

Ladder and cube

Problem

Student Solutions

Teachers' Resources