Keep your momentum going
Problem
You may have learned Newton's 2nd law of motion, "force is equal to the rate of change of momentum". In fluids, the rate of change of mass, $dm/dt$, often abbreviated $\dot{m}$, is important. Use the product rule to find the form of Newton 2 that includes the possibility of mass flow.
If the flow is "steady", i.e. the mass flow in to a certain volume equals the mass flow out, the formula you derived simplifies to $F = \dot{m}v$.
When we resolve this formula in any particular direction, we call it the "steady flow momentum equation".
A tank (pictured) has a chemical (density $800kg/m^3$) flow of 1kg/s going through from left to right. The inlet pipe has an area $100cm^2$, and the outlet pipe has an area $50cm^2$. If the inlet pressure is 1MPa, what is the output pressure? Hint: mass is conserved, and the mass flow in a pipe of area A with fluid velocity V is just $\dot{m} = \rho AV$.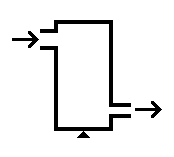
Can you see any structural problems that might arise with this tank?
Would it make a significant difference if the tank were aligned vertically or horizontally?
Getting Started
Student Solutions
Resolving forces and the resultant mass flows in the "x" direction, $\sum{P_x A_x} = \sum{\dot{m}V_x}$.
So $P_{in}A_{in} - P_{out}A_{out} = \rho A_{in}V_{in}(V_{out} - V_{in})$.
$\therefore P_{out}A_{out} = P_{in}A_{in} - \rho A_{in}V_{in}(V_{out} - V_{in})$.
but $A_{out}V_{out} = A_{in}V_{in}$ (conserve mass), so
$P_{out}A_{out} = P_{in}A_{in} - \rho A_{in}V_{in}^2(A_{in}/A_{out} - 1)$.
But, $\dot{m} = \rho A_{in}V_{in} \therefore V_{in} = \dot{m}/\rho A_{in}$
$\therefore P_{out} = (P_{in}A_{in} - \rho A_{in}(\dot{m}/\rho/A_{in})^2)(A_{in}/A_{out} - 1)/A_{out}$
$= (P_{in}A_{in} - (\dot{m})^2/\rho/A_{in})(A_{in}/A_{out} - 1)/A_{out}$
Entering the data we have, $P_{out} = 1999975Pa$.
There might be a structural problem with the tank because of the offset distance between the pipes, such that the pressure force in the pipes would generate a twisting moment. This was a problem in the Flixborough disaster.
