Just Opposite
Problem
Image
|
$A$ and $C$ are the opposite vertices of a square $ABCD$, and
have coordinates $(a,b)$ and $(c,d)$, respectively.
What are the coordinates of the other two vertices?
What is the area of the square?
How generalisable are these results?
|
Getting Started
Student Solutions
Just using coordinates and the clue in the original diagram there is a short and sweet solution sent in by Jo from Leeds.
By concentrating on the geometry, she made the algebra very simple. With the clue that $p-q = a-c$ and $p+q=b-d$ she was able to find the area of the square $ABCD$:
The inner square would have a side of $6-3 =3$.
The area of the tilted square is therefore $5 \times 5 - \frac{(5 \times 5)-(3 \times 3)}{2} =17 $ sq units and this can be generalised.
In the algebraic case.
Area $= (b-d)^2- \frac{((b-d)^2- (a-c)^2)}{2} $
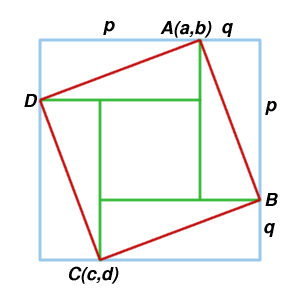
Michael Gray from Madras College solved the first part using vectors.
The midpoint of the square is given by $M=((a+c)/2, (b+d)/2)$. Hence
Teachers' Resources
Why do this problem?
This problem allows students to explore new ways to see (visualise) the 'tilted square' figure. It combines work on coordinates and area with possibel extensions into Pythagoras' theorem. There is the potential for different insights that can be utilised to invite discussion about different approaches.Possible approach
A visualisation can be grasped quite easily when someone points it out, but it is more satisfying and much better for the students' development if they gradually feel their way around the structure with moments of revelation.
Invite learners to create tilted squares of their own, identify coordinates of diagonally opposite corners. Can they usethese to help to find areas? Share ideas and generalisations as they arise.
Connections may take time to emerge and different insights might result in different approaches. For example the area of the tilted square might be found through considering one of the squares and a rectangle or seen as half way between the areas of the smaller and larger squares. Give space for learners to find their own visualisation and share different ideas and approaches.
One important configuration to watch for is this one:
Key questions
- Can you work form some specific cases to the general?
- How do the areas of the squares and rectangles relate?
- How do the coordinates of opposite coordinates relate to the dimensions of the inner and outer squares?
