Island hopping
What is the smallest number of ferry trips that Neda needs to take to visit all four islands and return to the mainland?
Age
11 to 14
Challenge level
Problem
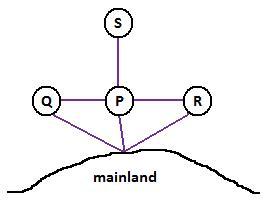
Neda decided to take the ferry from the mainland to visit the four islands $P$, $Q$, $R$ and $S$.
The island $Q$ can be reached by ferry only from island $P$ or from the mainland. Ferries connect islands $P$ and $R$, and each of them with the mainland. Island $S$ only has a ferry connection with island $P$.
What is the smallest number of ferry journeys that Neda needs to take in order to visit all the islands and return to the mainland.
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
To visit $S$ requires a journey from $P$ to $S$ and one back. To visit $P$, $Q$ and $R$ and return to the mainland requires at least $4$ journeys, so at least $2+4=6$ journeys are required to visit all four islands and return.
Image
