I'm Eight
When I went into a classroom earlier this week, a child rushed up to tell me she was 8 that day.
Well, Happy Birthday to everyone who has a birthday today!
This challenge is about finding a variety of ways of asking questions which have the answer 8.
You might think of 6 + 2, or 22 - 14, or...
Try to create examples that use all the different mathematical ideas that you know about.
Perhaps you could challenge yourself to find ways of making 8 that you think no-one else will have thought of.
If you are not 8 years old, you might like to use your age instead of 8.
Can you change the starting point of one of your solutions and then tweak it a bit to find another way of making 8?
We had over 70 solutions sent in for this task!
Tayla from Marion Primary School in Australia and Luna from Marner Primary School in England, sent in what they called “all the possible additions equalling 8”:
5+3 =8 3+5 =8 6+2=8 2+6=8 1+7=8 7+1=8 4+4=8
and then the subtractions:
9-1=8 10-2=8 11-3=8 12-4=8 13-5=8 14-6=8
PomPom from the Australian International School Malaysia extended the idea and used a division making 12:
6+6=12, -20+32= 12, 24$\div$2= 12
Micaela from the Westridge School for Girls went further by using more than two numbers to generate the solution:
For the number 8 I did 100 minus 48 minus 32 minus 4 minus 8 which equaled eight.
Now for a random age of 10 I did 87 minus 16 minus 11 then subtract 50. That's both of my answers.
Adelaide and Janeen also from Westridge used all four operations:
0+8=8 Eight minus eight equals zero, so eight plus zero must equal eight.
19-11=8 Eleven plus eight equals nineteen, so nineteen minus eleven must equal eight.
2x4=8 Eight divided by two equals four, so two times four must equal eight.
24$\div$3=8 Eight times three equals twenty-four, so twenty-four divided by three must equal eight.
2+6=8 If eight minus six equals two, then six plus two must equal eight.
99-91=8 Eight plus ninety-one equals ninety-nine, so ninety-nine minus ninety-one must equal eight.
1x8=8 Any number times one equals itself.
64$\div$8=8 Eight times eight equals sixty-four, so sixty-four divided by eight must equal eight.
3+5=8 Eight minus five equals three, so three plus five must equal three.
55-47=8 Eight plus forty-seven equals fifty-five, so fifty-five minus forty-seven must equal eight.
All the ways to make eight is infinite but these are just a few examples.
Sofia and Alicia also from Westridge produced fifty altogether but went further by using different operations in one calculation (click on the image to see it larger):
Noah, Oania, Jasmine, Nabil, Rayyan, Luna, Nibir, Rheshai, Arafat, Yasmiin, Sheum, Aadam, Haifa, Mahira, Faridah, Yunus, Ismat, Chloe, Maryam, Nabeeha, Qiyyama, Oania and Yusuf from Marner Primary School London sent in their solution, which also mentions how they knew those solutions:
96 divided by 12 equals eight. You can use inverse to check your answer as 12 x 8 = 96
100-92=8 I know this because 92+8=100
3x3-1=8 3x3 is 9 and -1 is 8.
A way to make 8 is when you have the number 100 and take away 92 because 100 -90=10 and 10-2=8!
2+6=8; 3+5=8; 4+4=8; 5+3=8: 6+2=8: 7+1=8; 4+4=8; 64 divided or shared by 8=8; 2+2+2+2=8
16÷2=8 I know this because there are 8 2's in 16.
A way is 96 divided by 12=8 that is the answer; 8+33-33=8
I know that you can make 8 by timesing 2 and 4 and that also will make 8; 7+1=8 I know this because 1+7=8; 100-92=8 I know this because 100-2=98 and when taking away, the first 2 numbers, you can switch those numbers around.
80 take away 72 equals 8; 5 add 3 equals 8 16 divide it by 2 equals 8 18 take away 10 equals 8; 4 add 2 add 2 equal 8 14 take away 6 equals 8; 1+7=8 8+0=8 5+3=8 3+5=8 0+8=8 double 4=8 2x4=8 11-3=8 7+1=8; 16 divided by 2=8
80÷10=8 because I counted in my head and it worked.
100-92=8 I know this because 8+92=100.
We had twenty three very different solutions in from the International School in Brussels. Some kept to the idea of making 8, others used their own ages as the target number. Click on any of them to download all twenty three in a Word Document. It's worth looking at them for the mathematics and the display styles. Thank you to Alessandro, Amo, Andrey, Arthur, Ben, Eleanor, Elise, Emma, Evie, Fede, Gonzalo, Heleen, Jack, Javier, Luna, Marina, Niko, Quinn, Raila, Suzy, TJ and Zoe.
| Here is Luna's, offering an original display and a variety of solutions: |
Here is Eleanor's, using ideas that are very different from others: |
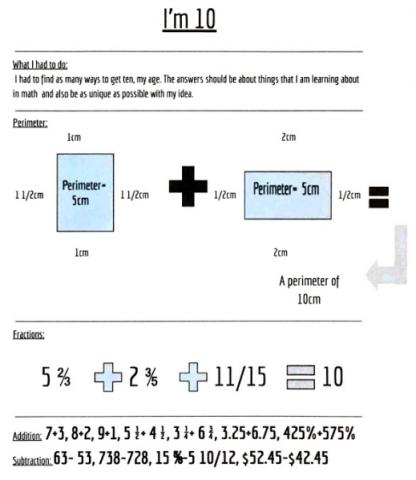
| Here is Evie's who separates ideas well. I like the idea of adding in "bonus" ones. It looks as Evie has enjoyed herself here! |
Here is TJ's. As well as an interesting display there's a lot of reversing going on. I think it's good to explore in this way! |
What a great response, so many thoughtful ideas for both the maths and the way of communicating it. Thank you all very much.
I'm Eight
When I went into a classroom earlier this week a child rushed up to tell me she was 8 that day.
Well, Happy Birthday to everyone who has a birthday today!
This challenge is about finding a variety of ways of asking questions which make 8.
You might think of 6 + 2, or 22 - 14 or...
However, try to create examples that use all the different mathematical ideas that you know about.
Perhaps you could challenge yourself to find ways of making 8 that you think no-one else will have thought of.
If you are not 8 years old, you might like to use your age instead of 8.
Why do this problem?
You could build further on children's natural curiosity by encouraging them to ask "I wonder what would happen when...?". If you are interested in pursuing curiosity in particular, then please see the 'Further note' at the bottom of this page.
Possible approach
Bring everyone together and ask how they felt being asked for another example, then another, then another... This way of working often encourages learners to challenge themselves in a way that asking for a particular number of examples all at once doesn't do. This raises children's awareness of the range of examples open to them rather than immediately opting for the first one that sprang to mind. (See John Mason's Open University course booklet Working On Your Own Mathematics, 2017, for more information about this approach.)
Invite pairs to share their ideas and record them on the board for all to see. You may find it helpful to try to group their suggestions into the four rules of number: addition, subtraction, multiplication and division, if applicable. The prompts you use will depend on the sorts of statements offered by the children, and how varied they are. If, for example, most statments use exactly two numbers, point this out and ask children to try to use three or four numbers to get 8. If they have used addition only, suggest that they could start with a biggish number and then take some away and then have to take some more away in order to end up with only 8. They may be motivated to create examples that they think no-one else will have thought of.
Allow plenty of time for pairs or individuals to work further on the task. A mini plenary might draw attention to those contributions that follow a particular pattern e.g. 1 + 7, 2 + 6 ... , encouraging children to write 'etc' to indicate that there were some more if they thought so. This activity could be left 'simmering' so that you come back to it later in the week and leave a space on your working wall for contributions in the meantime.
Key questions
Possible extension
Possible support
Further note
You may be interested in the following talks given by Professor Susan Engels, which focus on encouraging curiosity and are available on YouTube:The Rise and Fall of Curiosity - the extract from 23.50 to 37.15 on adult encouragement and teacher behaviour is particularly worth viewing;
The Hungry Mind: The Origins of Curiosity - the extract from 8.22 to 12.29 on children asking questions is especially useful.