Icosian game
This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only returning to the vertex you started at.
Problem
This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only- returning to the vertex you started at.
This is quite difficult to visualise in 3D so this problem involves drawing 2D skeletons of the five Platonic solids (known as Schlegel graphs) and using these to try to answer the challenge we have set you below.
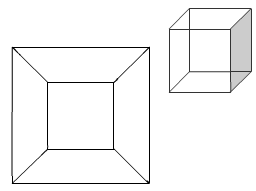
Schlegel graphs are very useful in studying molecular structure. It is as if all the edges were made of elastic and they have been stretched out to make the skeleton flat. Here is a cube and its Schlegel graph:
Can you sketch the skeletons on paper for the tetrahedron, octahedron, dodecahedron and icosahedron? When you think you have a skeleton - you can check your own answer by clicking to reveal the Schlegel graphs.
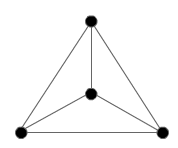
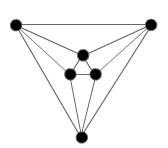
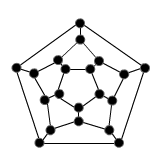
The problem is in two parts:
- to find the paths along the edges of the solids that enable you to visit every vertex and
- to describe the strategies you have used and what you discovered. For example: is the path unique?
These paths are called Hamiltonian Circuits after the Irish mathematician William Hamilton who also invented this game in 1857.
Student Solutions
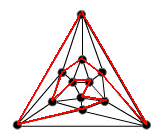
For the tetrahedron, I have:
I tested all Platonic solids: the tetrahedron, the cube, the octahedron, the dodecahedron and the icosahedron.
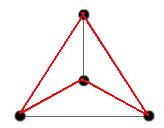
For the tetrahedron, there was simple - there were only four points to study. I obtained more possible arrangements, corresponding to different solutions. The other, not shown is to go on the outside circuit up to the last-but-one point, than to go to the centre and finally at the starting point. There are different solutions only if the start - finish is represented on the figure, otherwise this solution is obtained from the first by a rotation.
For the cube, I worked on an applet:
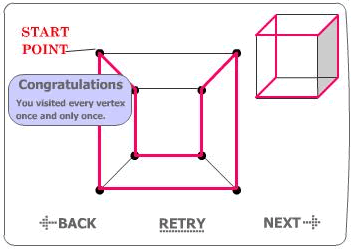
The strategy I used is the following: I go on the outer lines, up to the last-but-one point. Then I go through the inner one. I can use symmetrical combinations, obtaining more than one path.
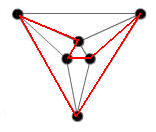
Looking at the octahedron, I take the same strategy as for the cube => there are many combinations.
For the dodecahedron, I worked on an applet, taking the same strategy as for the cube, the difference is that here there are more layers.
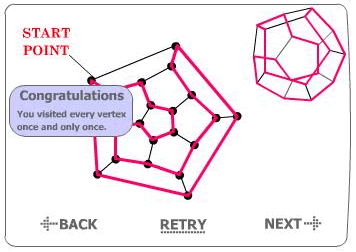
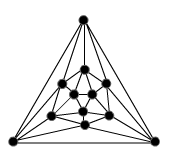
The last polyhedron I test is the icosahedron:
Here, I worked in the same manner as before, obtaining the figure shown. There are naturally more combinations.
