Happy halving
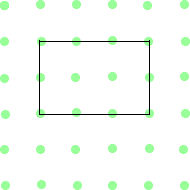
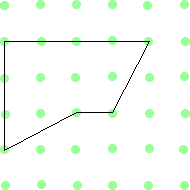
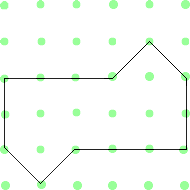
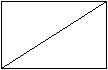
Can you split each of the shapes below in half so that the two parts are exactly the same?
Problem
Can you split each of the shapes below in half so that the two parts are exactly the same?
Image
|
Image
|
Image
| Image
|
Getting Started
You could print off this sheet with the shapes drawn so you can try out your ideas. Or you could make the shapes on a pegboard.
You might like to cut out the shapes first. Then you could try cutting each shape and checking to see whether the two parts are the same - perhaps you'll need to turn one of them round!
Student Solutions
Esin aged 7 from Mef School in Turkey sent these two solutions:
Image
| Image
|
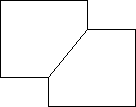
Dost, also 7 from the same school, sent alternative answers:
Image
| Image
|
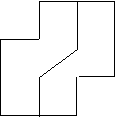
We also received this solution from Elizabeth, who goes to Warren Rd Primary School
Aoibheann and Padraic from Cloghans Hill NS in Ireland sent in this very good explanation.
The first shape (like a rectangle) you split in two by drawing a line through the middle.
The second shape (like two squares overlapping) you can split two ways, diagonally through from left to right, top to bottom OR accross where they overlap diagonally.
The third shape which is irregular, you cannot halve as there are five points in length on one side and four on another with another one point in a different place therefore although you could use the two diagonal lines to match each other, you have one point hanging out over one edge and you have one point too few on the other.
The fourth shape (which looks like house designs) you can halve easily by drawing a horizontal line accross the middle of both making the same shape on the top and the bottom.
Thank you for those solutions, there are still others that may be found!
Teachers' Resources
Happy Halving
Can you split each of the shapes below in half so that the two parts are exactly the same?
Image
| Image
|
Image
| Image
|
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support