Get cross
Problem
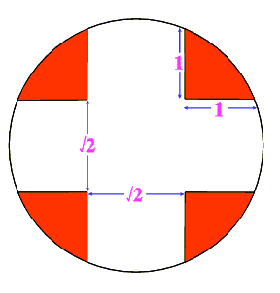
A white cross is placed in a red disc as shown and the resulting
figure is symmetrical.
What is the area of the disc still showing?
Student Solutions
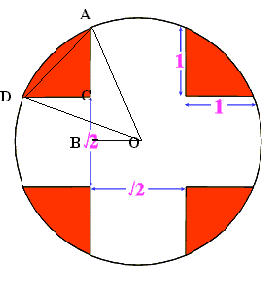
Using the cosine rule to find $\angle AOD$ we have $AC=CD=1$ and so $AD = \sqrt 2$ and hence
$$\cos \angle AOD = {{OA^2 + OD^2 -AD^2}\over 2OA.OD} = {1 \over \sqrt 2}.$$
Hence $\angle AOD = 45$ degrees.
The area of the triangle $AOD$ is
$${1\over 2} OA \times OD \times \sin \angle AOD = {\sqrt 2 \over 4}(2 + \sqrt 2).$$
To find the area of the minor segment $AD$ we subtract the area of triangle $AOD$ from the area of sector $AOD$ which gives
$${\pi \over 8}(2 + \sqrt 2) - {\sqrt 2 \over 4}(2 + \sqrt 2).$$
To get the total red shaded area we now add the area of triangle $ACD$ and multiply by $4$ which gives:
$$4[{\pi \over 8}(2 + \sqrt 2) - {\sqrt 2 \over 4}(2 + \sqrt 2)+ {1\over 2}]={\pi \over 2}(2 + \sqrt 2)- 2\sqrt 2 \approx 2.535 \rm {\ sq. \ units} .$$
