Funny Factorisation
Using the digits 1 to 9, the number 4396 can be written as the product of two numbers. Can you find the factors?
Problem
Funny Factorisation printable worksheet
Some 4 digit numbers can be written as the product of a 3 digit number and a 2 digit number using each of the digits $1$ to $9$ once, and only once.
The number $4396$ can be written as just such a product.
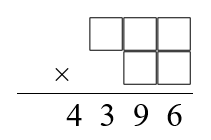
Can you find the factors?
Maths is full of surprises!
The numbers $5796$ and $5346$ can each be written as a product like this in two different ways.
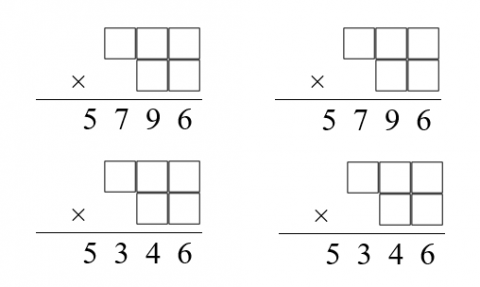
Can you find these four funny factorisations?
Extension
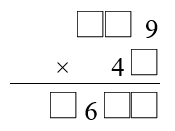
There are two more funny factorisations to find, using each of the digits $1$ to $9$ once, and only once.
Can you fill in the blanks in the multiplication below to find one of them?
If you know a bit about computer programming, you may wish to write a program to find the final funny factorisation.
Getting Started
Gabriel's Problem and Counting Factors might be good problems to try before looking at this one.
If you know the prime factors of a number, how can you work out which two-digit numbers are factors?
It might help to draw a factor tree.
If you'd like some help with the extension, click below
What is the largest that the four-digit number can be?
What is the smallest that the two-digit number can be?
What does this tell you about the three-digit number?
Now it might be helpful to think about the units digits.
Student Solutions
Some 4 digit numbers can be written as the product of a 3 digit number and a 2 digit number using the digits 1 to 9 each once and only once.
Well done Sally Nelson and Sarah Dunn, S2, Madras College, St Andrew's for finding altogether six funny factorisations, but there is one more. It is now a Tough Nut to find the last one. You might like to write a computer program to find all seven funny factorisations or you might come up with a different method. Let us know.
The number 4396 = 2 × 2 × 7 × 157 and there are not many possible combinations. By trial and error we get 4396 = 28 × 157.
The number 5796 = 2 × 2 × 3 × 3 × 7 × 23.
So 5796 = (2 × 3 × 7) × ( 2 × 3 × 23) or (2 × 2 × 3) × (3 × 7 × 23) amongst other possibilities which don't turn out to be 'funny'.
In this way we find the two funny factorisations: 5796 = 42 × 138 and 5796 = 12 × 483.
Similarly 5346 = 2 × 3 5 × 11 and the funny factorisations are:
5346 = 27 × 198 and 5346 =18 × 297.
Here you must use the digits 1 to 9 once, but only once, to replace the stars and complete this multiplication example.
| * | * | 9 | |
| $\times$ | 4 | * | |
| --- | --- | --- | --- |
| * | 6 | * | * |
Firstly I found out the possible solutions for the top row. It could not be a number above 250 or below 100 and it had to end in a 9. The number could not have a 4 or a 6 or another 9. The only possibilities were 129, 139, 159, 179, 189, 219 and 239. So I tried these numbers with every 2 digit number beginning with a 4 until I found the answer 159 × 48 = 7632.
Extension
We asked you to find all of the funny factorisations of 4-digit numbers which use all of the digits 1 to 9. We received two Python programs, one from Chris from Belmont, Massachusetts, USA and one from Ryan. Ryan's code sticks to the original problem, but Chris worked on a further extension. Chris wrote:
I did the activity and then I got curious, what if there are funny factorizations with 3 digits times 2 digits equals 5 digits? So I wrote some python code. The program starts by making a empty list and then the for loops are for sifting through every possibility. Inside the for loops it adds all the digits of the numbers (and their multiple) in the list. It then sorts the list and checks if every number in the list is unique. If so it prints out the funny factorization.
This is the output of Chris's code. Notice that the digits 0 to 9 are now used:
297×54=16038 345×78=26910 367×52=19084 396×45=17820 402×39=15678 495×36=17820 594×27=16038 715×46=32890 927×63=58401
Click to see Chris's code. Can you explain what each line does?
for j in range (10,100):
list1=[]
if(len(str(i*j))==5):
list1.append(int(str(i)[0]))
list1.append(int(str(i)[1]))
list1.append(int(str(i)[2]))
list1.append(int(str(j)[0]))
list1.append(int(str(j)[1]))
list1.append(int(str(i*j)[0]))
list1.append(int(str(i*j)[1]))
list1.append(int(str(i*j)[2]))
list1.append(int(str(i*j)[3]))
list1.append(int(str(i*j)[4]))
list1.sort()
if (list1 == list(set(list1))):
print(str(i)+"x"+str(j)+"="+str(i*j))
Click to see an explanation. Could you think of any ways to make the code more efficient?
Then, for each possible i and j (or each possible two digit number and three digit number combination), Chris creates an empty list called list1. This is really a space to store information, like a blank piece of paper.
Chris's program then calculates i*j (i multiplied by j), and checks whether it has 5 digits. If it does, then all of the lines of code beginning "list1.append..." are executed. If i*j doesn't have 5 digits, then it moves straight on to the next i and j.
Assuming i*j has 5 digits, Chris's program then "appends" all of those 5 digits to the list - like writing them down on a piece of paper. It also put the individual digits in i and j in the list (in fact it puts those on first). It then sorts the list in ascending order. Then, Chris needs to check whether there are any duplicates on the list. He does this by turning it into a "set" - which is free of duplicates - and then turning it back into a list so that it can be compared with the original list. If the program finds that removing duplicates has not changed the list, then it prints out the funny factorisation before moving on to the next i and j.
Ryan's code works in a different way - and notice that Ryan's final numbers are still 4 digits long. Click to see Ryan's code. Can you explain how it works?
L=[1,2,3,4,5,6,7,8,9]
a=0
a=L[j]
M=L[:]
M.pop(j)
for k in range(8):
b=0
b=a+10*M[k]
N=M[:]
N.pop(k)
for l in range(7):
c=0
c=N[l]
O=N[:]
O.pop(l)
for m in range(6):
d=0
d=c+10*O[m]
P=O[:]
P.pop(m)
for n in range(5):
e=0
e=d+100*P[n]
f=b*e
Q=P[:]
Q.pop(n)
for o in range(4):
f=0
f=Q[o]
R=Q[:]
R.pop(o)
for p in range(3):
g=0
g=f+10*R[p]
S=R[:]
S.pop(p)
for q in range(2):
h=0
h=g+100*S[q]
T=S[:]
T.pop(q)
for r in range(1):
i=h+1000*T[r]
if b*e==i:
print b,e,i
Click to see an explanation. Could you think of any ways to make the code more efficient?
For each value of a, which will represent the second digit of the two-digit number, Ryan's program then makes another list M which begins life the same as L (using the code M=L[:]). Ryan then uses M.pop(j) to remove the jth element of M from the list - which was a. So M is the list of possible digits for the first digit of the two-digit number, which doesn't contain a, because a is the last digit.
There are only 8 digits in M, so for each value of a, there are 8 options for the two-digit number. Ryan's program lets k run from 0 to 7 and chooses the kth digit from M to create the two-digit number, which is called b and comes from doing a plus 10 times the kth digit in M.
Ryan's program then makes a copy of the list M (called N) to store the possible numbers that the third digit of the three-digit number could be. It removes the kth digit from N, because that one shouldn't appear again. This process continues - all possible three-digit number are chosen using all only digits that are not in the two-digit number. Then, for each two- and three-digit number pair with no digits in common, all possible four-digit numbers are checked using the remaining four digits.
Finally, for each two-digit, three-digit and four-digit number combination which use the digits 1 to 9, Ryan's program checks if the four-digit number is the product of the other two - and prints it if it is.
Which program do you find easier to understand? Could Ryan and Chris have used comments to make their code more human-readable? Which is more similar to your method? Which do you think is more efficient for a computer to run?
Teachers' Resources
Why do this problem?
This problem shows the value and power of factor trees and prime factorisation for finding solutions to a problem that may at first glance seem almost impossible! A systematic approach is all that is needed...
Possible approach
This printable worksheet may be useful: Funny Factorisation
Draw the first product on the board, and explain that the missing cells contain the digits 1, 2, 5, 7 and 8 in some order so that the whole calculation uses each of the digits 1 to 9 once and only once:

Give students a bit of thinking time to make a plan for how they might solve the problem, and then bring them together to discuss approaches. Some might suggest working out which pairs of numbers multiply together to give a 6 in the units column. Others might think of finding all the factor pairs that multiply to give 4396 and looking for a pair that uses the appropriate digits. (If no-one suggests the second method, you could give them a hint that this might be a good approach, by drawing attention to the title of the problem.)
Students will need to think about how to combine the prime factors of 4396 to make 2-digit numbers, and then work systematically through the possibilities to find a pair that uses the available digits. Once they have tackled this first challenge, you can let them loose on the rest of the funny factorisations.
Key questions
Does it help to draw a factor tree?
If you know the prime factors of a number, how can you work out which two-digit numbers are factors?
Possible support
Gabriel's Problem and Counting Factors might be good problems to try before looking at this one.
Possible extension
The "fill in the blanks" funny factorisation requires a different sort of systematic reasoning to complete.
A challenging extension for students who know a bit about computer programming might be to write a program that finds all seven funny factorisations.
