Flight Path
Use simple trigonometry to calculate the distance along the flight
path from London to Sydney.
Problem
You only need elementary trigonometry to do this question if you use the guidance given in the hints.
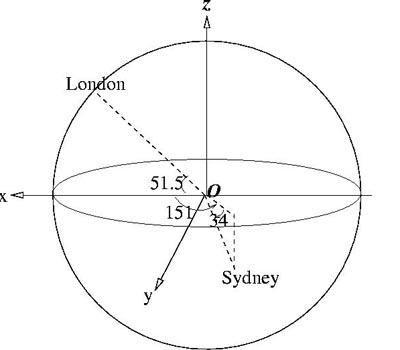
London is at longitude $0^o$ and latitude $51.5^o$ North and Sydney at longitude $151^o$ East and latitude $34^o$ South. Taking the earth to be a sphere with radius 6378 kilometres, calculate the distance between London and Sydney.
If the flight path is the shortest route at an altitude of 6 kilometres calculate the distance along the flight path.
Getting Started
Image
|
You need to show that if a place has (latitude, longitude) = $(p,q)$ then its coordinates are $$(R \cos p \cos q, R \cos p \sin q, R \sin p).$$ |
Image
|
Steps in the
calculation
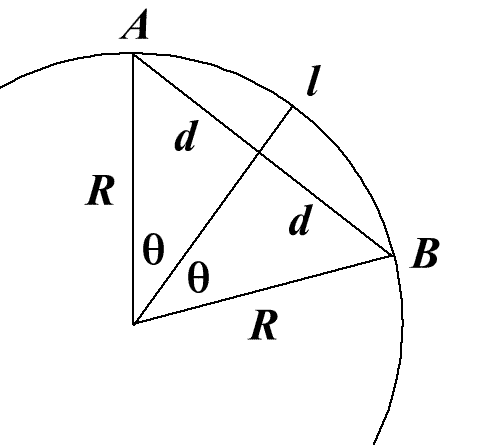
We need the distance $l$ on the surface between A and B.
First calculate the three-dimensional coordinates of A and B
from the latitude and longitude of the two points.
Then calculate the distance $2d$ (imagine a tunnel straight
through the earth from A to B) using Pythagoras Theorem.
Use $R$, the radius of the Earth, and $d$ to find the angle
$\theta$ radians where $$\sin \theta = {d\over R}.$$ Calculate the
arc length $l$.
|
Student Solutions
The solution here uses 3D Cartesian coordinates and the cosine rule. For a similar problem with a solution that uses scalar products of vectors see Air Routes. A third method is to draw an altitude of the isosceles triangle with London, Sydney and the origin as vertices and use the trigonometry of the right-angled triangle.
Image

|
This solution comes from Andrei from Tudor Vianu National College, Bucharest, Romania.
To solve this problem I see that the data are given in spherical coordinates, but I need to work in Cartesian coordinates.
I choose the Cartesian system of coordinates with the origin at the centre of the Earth, with the $xy$ plane - the equatorial plane, and the $z$ axis directed towards the North Pole. The spherical system of coordinates has the origin at the same point as the Cartesian one, i.e. at the centre of the Earth. Let the angle $p$ measure the latitude (0 at the equator and $\pi/2$ at the North
Pole), i.e. it is the angle between the position vector of the current point $P$ and the plane $xOy$. Let the angle $q$ measure the longitude (in respect to the axis $Ox$), i.e. it is the angle between the projection of the position vector of point $P$ on the plane $xOy$ and the $x$ axis. So the 3D coordinates in terms of the angles of latitude and longitude are: $$x = R \cos p \cos q, y = R \cos
p \sin q, z = R \sin p.$$
|
London has longitude 0 and latitude 51.5 degrees North and Sydney has longitude 151 degrees East and latitude 34 degrees South. The corresponding angles for London and Sydney are: $p_L = 51.5, q_L = 0, p_S = -34, q_S = 151$.
The distance between the two cities, measured on the line joining them and passing through the interior of Earth, is: $$d^2 = R^2 ((x_L - x_S)^2 + (y_L - y_S)^2 + (z_L - z_S)^2).$$ Both cities are situated on the sphere, and this means there exists a great circle of the Earth passing through both of them. Let $\alpha$ be the angle between the two cities, and having the vertex at the centre
of the Earth (defined on the great circle specified above). This angle can be found using the cosine rule for the isosceles triangle defined by the position of London, the centre of Earth and the position of Sidney: $$d^2 =R^2 + R^2 - 2R^2 cos \alpha$$ So, $$\cos \alpha = {2R^2 - d^2\over 2R^2}.$$ The distance between the two cities measured on the surface of the Earth, along the great circle, is
$R\alpha$, where $\alpha$ is measured in radians. Let it be $L_1$, then: $$L_1 = R\cos^{-1}{(2 - (x_L-x_S)^2 - (y_L-y_S)^2 - (z_L-z_S)^2) \over 2}.$$ The other distance is calculated adding 6 km to the radius of the Earth, and it will be $L_2$.
The numerical results are: $\alpha = 2.66$ radians and, on the surface of Earth, the distance, to the accuracy of the measures used, is: $$L_1 = 17000 \ {\rm km}.$$ At the altitude of 6 km the distance $L_2$ is about 16 kilometres more than $L_1$.
The results are in reasonable agreement with the distance: 16972 km according to Google Earth and 16997 km on http://portcanal.co.uk/cgi-bin/diser.pl?a=London&b=Sydney
The problem Over the Pole shows that the great circle distance is shorter than the path along a line of latitude for two points with the same latitude.
Teachers' Resources
Image

|
A model to demonstrate
latitude and longitude
Cut 2 discs of cardboard.
Cut a radial slit in each so that they slot together as
shown.
Mark your chosen cities and their angles of latitude. In the
illustration London at $51.5^o$ North and Sydney at $34^o$ South
are shown.
Cut off a small segment at the South Pole so that the model
stands up.
Adjust the angle between the two planes in the model to show
the difference in their angles of longitude.
|
Image

|
Take the origin at the centre of the earth, the x-axis through
the Greenwich Meridian at the equator, the y-axis through longitude
$90^o$ East at the equator and the z-axis through the North
Pole.
London is approximately on the Greenwich Meridian so the 3-D
coordinates of London are $(R\cos 51.5^o, 0, R\sin 51.5^o$).
|
As an extension to this question you might like to calculate
the distance between Cape Town ($18^o$E, $34^o$S) and Sydney
($151^o$E, $34^o$S) along the great circle and find how much
shorter it is than the distance around the line of latitude
$34^o$S.
