Flight of the Flibbins
Blue Flibbins are so jealous of their red partners that they will not leave them on their own with any other bue Flibbin. What is the quickest way of getting the five pairs of Flibbins safely to the new planet?
Problem

The last ten Flibbins who live on the planet Filbert are in trouble. They are under threat from a cactus-like creature whose spines are fatal to the Flibbins and who are due to start their annual moult in a few days time!!
The Flibbins have found a neighbouring planet that is uninhabited and where they can survive if they can get there safely. However, they have some problems with organising their emigration.
Firstly, they only have one spacecraft that will carry at most one pilot and two passengers. Of course, the spacecraft can't fly (either to the new planet or back from it) without a pilot, which can be any of the Flibbins!
Secondly, the ten Flibbins each have a partner of the opposite colour. The blue Flibbins are all very protective of their red partners, so if the blue partner is not present (on either planet or the spacecraft), there should be no other blue Flibbins with their red partner (but other red Flibbins are fine). Red Flibbins, however, are not so protective of their blue partners.
What is the quickest way of getting the five pairs of Flibbins safely to the new planet?
Getting Started
Is it possible to send a mixture of blue and red Flibbins across in the boat together?
You can always leave red Flibbins alone together.
Student Solutions
Betsy, from the Mount School in York, was able to work out how to start the process going:
Image

| The red pilot flies two red Flibbins to the new planet, two stay there and the red pilot flies back to Filbert. | Image

|
Image

| The red pilot flies the other two red Flibbins to the new planet, who stay there, making a total of four, and the red pilot flies back to Filbert. | Image

|
Eleanor, from the Methodist Girls' School, Singapore, sent in this correct solution:
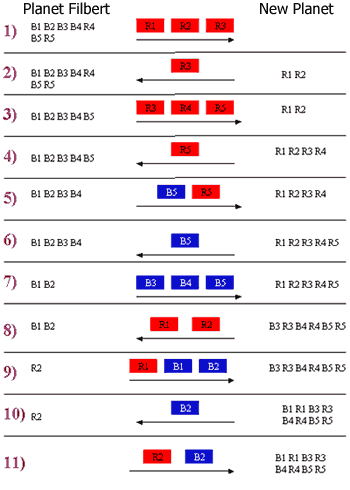
Let the blue Flibbins be B1, B2, B3, B4 and B5, and the red Flibbins be R1, R2, R3, R4 and R5, whereby B1 and R1 are a pair, B2 and R2 are a pair and so on so forth.
Firstly, as Betsy mentioned, 3 Flibbins should go on the first trip. Thus R1, R2 and R3 set off on the first trip.
R3 then becomes the pilot, and returns to planet Filbert to fetch R4 and R5. Therefore, R3, R4 and R5 reach the new planet where R1, and R2 are in.
R5 then becomes the pilot, and returns to fetch B5.
Upon reaching, B5 cannot stay on the new planet with R1, R2, R3, and R4 as B1, B2, B3 and B4 (respectively) will be jealous. Hence, B5 becomes the pilot, and returns to planet Filbert to fetch B3 and B4.
B3 and B4 arrive with B5. Thus, R1 and R2 have to leave on the spacecraft, to avoid B1 and B2 from becoming jealous.
B1, R1 and B2 then set off for the new planet, leaving R2 behind on planet Filbert. This is possible as B1 will not be jealous (as he is accompanying R1), and neither will B2 be jealous (as there are no blue Flibbins left on planet Filbert).
B2 then becomes the pilot, and returns to fetch R2.
Hence, in total, there are 11 trips, out of which 5 are return trips.
Alternatively, on the 5th trip, R5 could also fetch another blue Fibbin, other than B5. This is possible as B5 will not be jealous (because it is accompanying R5). However, if say R5 also fetched B4, on the 6th trip, both B4 and B5 will be pilots. Thus, this will not change the least amount of the total number of trips made, which is 11.
Joel of Raffles Junior College also gave a solution involving 11 journeys, together with a nice clear diagram.
Originally, it wasn't made clear that the spacecrat needed a pilot. Zac, Sammy and Robert, from Bentley Park College, Australia, sent in this solution to the version of the problem without a pilot:
We have solved this puzzle and this is how. By sending three red Flibbins on the 1st trip, three blue Flibbins on
the 2nd trip. On the 3rd trip we sent one red and one blue Flibbin and again the same on the 4th. In total 4 trips (plus return journeys) were needed.
1st= Red, Red, Red
2nd= Blue, Blue, Blue
3rd= Red, Blue
4th= Red, Blue
Thank you and well done to everyone who submitted solutions to this problem!
